質の高い数学の指導とは何ですか？そしてなぜそれが重要なのですか？
2ページ目: 標準に基づいた数学カリキュラム
専門家の間では、数学の最も効果的な教授法をめぐる議論は、決して新しいものではありません。過去の数学のカリキュラムは、規則や手順の指導に加え、計算能力の育成にも重点を置いていました。こうした手続き的な知識の重要性は疑いようもありませんが、生徒が学んだことを現実世界の状況や場面で正しく応用するためには、概念的な理解も不可欠です。言い換えれば、教師は数学の概念と手順の両方を指導し、両者の関連性を明確に示さなければなりません。
従来のカリキュラムも同様に、内容が浅く、知識とスキルの結びつきが欠け、計算手順に偏重し、エビデンスに基づく実践がほとんど活用されていないと批判されてきた。これらの欠点に対処するため、教育者は以下の点を実施することが求められている。 基準に基づいたカリキュラムこれらは数学的原理の概念的理解に焦点を当てています（ 現在も将来も、）とそれらの関係を数学の標準によって概説されているように理解するのであり、手続き的知識（ の).
多くの州では、生徒が大学進学や就職に必要なスキルを習得できるよう、より厳格な基準を導入しています。数学の場合、ほとんどの州では、これは数学に関する共通コア州基準（CCSSM）を意味しており、これは生徒が各学年で習得することが期待されるスキルと概念を概説しています。CCSSMは具体的には、以下のことを行います。
- 現在の州基準の強みを活かす
- 他の優秀な国で使用されている教育実践を参考にして、すべての生徒がグローバル経済と社会で成功できるように準備します。
- 証拠に基づいている
- 大学や仕事での期待に合致している
- 明確で、理解しやすく、一貫性がある
- 厳格な内容を取り入れ、高次のスキルを通じて知識を応用することを要求する
- 現実世界の問題の利用を奨励する
ご参考までに
政治が絡む多くの分野と同様に、共通コア州基準（CCSS）をめぐっても多くの論争が巻き起こっています。しかし、それらに対する異議の大部分は、誤解や誤情報に基づくものでした。事実はこうです。CCSSは、州教育長協議会（CCSSO）と全米州知事協会（NGA）が後援する州主導の取り組みの一環として策定され、米国の学校に共通の学習基準を策定することを目指しています。この取り組みは、教師、管理者、専門家の意見を参考に策定され、米国および国際的に使用されている最良の指導モデルを反映しています。
Diane Pedrotty Bryant が CCSSM の目的について説明します (時間: 2:20)。
ダイアン・ペドロッティ・ブライアント博士
学習障害および困難のための数学研究所プロジェクトディレクター
テキサス大学オースティン校
トランスクリプト：ダイアン・ペドロッティ・ブライアント博士
数学における共通コア州基準は、各州でより標準化された数学基準を提供するための非常に優れた試みです。学校の数学カリキュラムについては、専門団体や全米数学諮問委員会から、各学年で何をカバーしようとしているのかという批判が数多く寄せられています。「幅は1マイル、深さは1インチ」という諺がありますが、これは教室での数学指導において、あまりにも多くのことをしようとしていることを示唆しています。ですから、この基準は、特定の数学のトピックについて、より焦点を絞った一貫性のある基準を提供すること、そしてこれらのトピックが発達段階に適切であること、数学のトピックの学習の進行に沿っていること、そして概念的理解と手順的知識の両方を養うことを確実にすることを目的としていると私は考えています。授業では時として欠けている数学の概念的理解を、生徒がより深く伸ばせるように支援することに真に重点が置かれています。
また、この基準は数学のカリキュラムや数学指導のための具体的な介入策を定めるものではないことを明記しておくことが重要だと思います。各学区の指導者が、それぞれの学区のガイドラインとカリキュラムに従って基準を運用していくことが重要です。この基準は、教室における介入策やカリキュラムを規定するものではなく、各学年で指導すべき重要な数学的概念とは何か、そして教師がこれらの基準を調整するのに役立つ学区のプログラムにはどのような教材があるかを判断するための指針となるものです。
CCSSM は、生徒が数学の内容に取り組む方法を説明した 8 つの数学実践基準と、各学年で生徒が学ぶべき内容を概説した数学内容基準で構成されています。
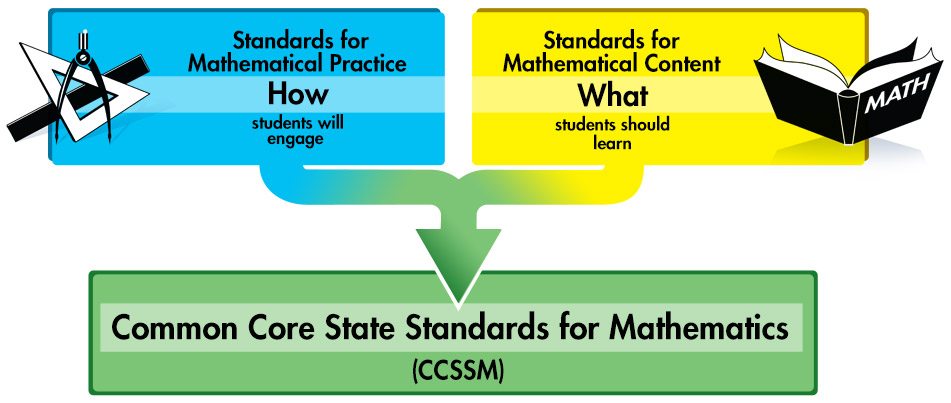
この図は、Common Core State Standards for Mathematics（CCSSM）を構成する要素を示しています。2つの長方形のボックスは、個々の基準と、それらが生徒の学習に与える意図的な効果を表しています。これらは矢印で結ばれており、そのすぐ下にある「Common Core State Standards for Mathematics（CCSSM）」と書かれた大きな長方形につながっています。
左上には「数学実践基準：生徒の取り組み方」と書かれた青いボックスがあり、コンパス、三角定規、定規が描かれています。右上には「数学内容基準：生徒が学ぶべきこと」と書かれた黄色いボックスがあり、開いた数学の教科書が描かれています。青いボックスと黄色いボックスは底部で繋がって矢印を形成し、色が混ざり合って緑色になります。緑色は、これらが流れ込む共通コア州数学基準（CCSSM）のボックスの色です。
数学実践の基準
CCSSMの数学実践基準は、 全米数学教師評議会 (NCTM) と 国立研究評議会各学年で習得する必要がある内容に生徒がどのように取り組むかを説明します。以下の表に記載されている8つの実践はすべての学年に適用できますが、生徒の年齢や発達段階に応じて適用方法が異なる場合があります。
全米数学教師評議会 (NCTM)
用語集
国家研究評議会 (NRC)
用語集
| CCSSM数学実践基準 |
|---|
| MP1: 問題を理解し、解決に努めます。 MP2抽象的かつ定量的に推論する。 MP3実行可能な議論を構築し、他者の推論を批評します。 MP4: 数学を使ったモデル化。 MP5: 適切なツールを戦略的に使用します。 MP6: 精度に注意してください。 MP7: 構造を探して活用します。 MP8: 繰り返される推論における規則性を探し、表現します。 |
数学の内容に関する基準
CCSSM数学内容基準は、生徒が習得すべき知識とスキルを規定しています。これらは学年ごとに異なる領域に分かれています。
幼稚園～8年生
幼稚園から中学11年生までの基準はXNUMXの領域に分類されています。以下の表は、これらの領域と、それぞれの対象となる学年を示しています。
| K | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | |
| カウントと基数 |  |
||||||||
| 演算と代数的思考 | |
|
|
|
|
|
|||
| 10進数の数と演算 | |
|
|
|
|
|
|||
| 測定とデータ | |
|
|
|
|
|
|||
| ジオメトリ | |
|
|
|
|
|
|
|
|
| 数と計算 – 分数 | |
|
|
||||||
| 比率と比例関係 | |
|
|||||||
| 記数法 | |
|
|
||||||
| 式と方程式 | |
|
|
||||||
| 統計と確率 | |
|
|
||||||
| 機能 | |
ハイスクール
CCSSMの目的は、学生が数学の概念と手順を徹底的に理解し、その知識を新しい状況に適用する能力を養うことで、大学や職場で活躍する準備をすることです。この能力は、 一般化学年別に編成されたK-8基準とは異なり、高等学校基準は概念的なカテゴリーに分かれています。
- 数と量
- 代数
- 機能
- モデリング
- ジオメトリ
- 統計と確率
ご参考までに
当学校区の CCSSMウェブサイト これらの規格についてさらに詳しく知るには、こちらが参考になります。特に以下のリンクは興味深いかもしれません。
- 数学実践の基準
- 数学の内容に関する基準
- あなたの州の基準 (お住まいの州が CCSSM を採用しているかどうかを確認するには、このリンクをクリックしてください。)
カリキュラム教材
知ってますか？
米国教育省は、標準に基づいた模範的な数学プログラムを数多く特定しています。 詳細についてはリンクをクリックしてください.
必要な基準に基づいたカリキュラムを教えるために、教師は カリキュラム教材つまり、生徒の学習プロセスへの参加を促すために設計された様々なリソース、アイテム、またはツールのことです。これらのカリキュラム教材には、教科書、補助教材、アクティビティが含まれます。しかし、教室で使用する前に、教師（または学校チーム）は、新しい教材だけでなく既存の教材も評価し、州の基準に準拠し、多様な学習者のニーズに対応していることを確認する必要があります。幸いなことに、MLDの生徒に効果的であることが証明されている指導上の特徴がいくつかあり、数学が苦手な他の生徒にも有益となる可能性があります。
| 指導上の特徴 | 案内質問 |
| 明確な目標 | レッスンの目標は、生徒の習熟度を簡単に判断できるほど具体的ですか? |
| 単一のスキルまたは概念の指導 | レッスンは単一のスキルまたは概念に焦点を当てていますか? |
| 教具の使用 | レッスンでは、概念や手順を説明し、数学の問題解決を支援するために具体的な物体の使用を促進していますか? |
| 指導アプローチ | レッスンには、明示的かつ体系的な指導など、証拠に基づいた指導戦略の使用が組み込まれていますか? |
| 教師の例 | レッスンでは、教師がスキルや概念を説明するために使用できる十分な例が提供されていますか? |
| 練習の機会 | レッスンには、生徒が概念を理解したりスキルを習得したりするのに役立つ十分な練習問題が含まれていますか? |
| 前提スキルの確認 | レッスンでは、新しいスキルを習得するために必要な前提スキルを復習しますか? |
| エラー訂正と修正フィードバック | レッスンには、生徒が問題を正しく解決できるようにするための体系的な手順を含む修正フィードバックが組み込まれていますか? |
| 語彙 | レッスンでは重要な語彙を特定し、教師がそれらの用語をどのように紹介し定義すべきかを説明していますか? |
| 戦略 | レッスンには、生徒が問題を解決するために使用できる段階的な認知戦略（教師によって明示的に教えられる）が含まれていますか? |
| アセスメント | レッスンでは、教師が生徒の学習状況やスキルまたは概念の習得度を個別に評価する機会が提供されますか? |
Bryant、Bryant、Kethley、Kim、Pool、Seo (2008) より改変。
教師は、MLDの生徒のニーズに対応するカリキュラム教材を確実に提供するように、ELLの生徒に対しても同様の配慮をしなければなりません。以下の文書では、ELLに特化した詳細なガイドラインを提供しており、教師はカリキュラム教材を評価し、指導計画を策定する際に活用できます。
留意すべき重要な点は、教科書開発者が自社製品が現在の数学の基準や特定の州の基準に準拠していると主張することに強い意欲を持っていることです。教師は、そのような主張を鵜呑みにせず、カリキュラム教材を自ら評価し、その価値を見極める必要があります。カリキュラム教材が州の基準に準拠していない場合、あるいは多様な学習者のニーズに対応できていない場合、教師はそれを補足する必要があります。キム・ポールセンがカリキュラムの補足についてさらに詳しく説明します（時間：1:38）。
キム・ポールセン、EdD
特別支援教育准教授
バンダービルト大学
トランスクリプト: キム・ポールセン、EdD
一つすべきことは、学区が選定したカリキュラムを確認し、その学年で数学にどれだけの時間が割かれているのかを確認することです。そして、そのカリキュラムで何ができるでしょうか？全てをカバーできるでしょうか？ほとんどの場合、答えは「いいえ」です。カリキュラムの教材が適切に設計されていないのではなく、時間が足りず、練習も十分に行われていないことが原因です。例えば、1年生の授業では、数学の教科書の1～2ページしか理解していない生徒は、それを理解していることを期待されますが、実際にはそうはなりません。そのため、補助教材を用意することが役立ちます。学区全体で利用している出版社の教材や、ウェブサイトで見つけたり、生徒の役に立つ様々なテクノロジーゲームを購入したりすることで、補助教材を見つけることができます。理解に苦しんでいる生徒や、ある概念を理解できなかった生徒を見極め、その理由を探り、教材を見つける必要があります。そして、その概念をすでに習得している生徒のことを考えてみてください。もう少し指導が必要な生徒と指導している間、彼らには何をさせるでしょうか？ すでに概念を理解している生徒と指導する際には、ただ雑用をさせるのではなく、より高度な思考力に焦点を当てた教材を用意する必要があります。
ご参考までに
教師は、学習に苦労している生徒のニーズに応える努力をしながらも、数学が得意な生徒を見落としてはなりません。学習内容を強化する活動を含むカリキュラム教材は、これらの生徒が学習分野をより深く掘り下げ、数学的プロセスをより洗練された方法で応用する能力を養うのに役立ちます。
