¿Qué prácticas basadas en evidencia de instrucción de matemáticas pueden emplear los maestros?
Página 5: Representaciones visuales
Las representaciones visuales son otra estrategia basada en evidencia que ayuda a los estudiantes a aprender conceptos abstractos de matemáticas y a resolver problemas. Más que tratarse sencillamente de una foto o una ilustración detallada, una representación visual—a menudo conocida como una representación esquemática o un diagrama esquemático—es una representación precisa de las cantidades y relaciones de un problema matemático. El propósito de esta representación visual es ilustrar el entendimiento de un estudiante del problema y ayudarlo a resolverlo correctamente. Por ejemplo, en la foto a la derecha, una estudiante usa una representación visual—aquí, una gráfica circular—para aprender sobre las fracciones equivalentes. A pesar del hecho de que los maestros implementan esta estrategia en los primeros grados para ayudar a los estudiantes a aprender hechos básicos de matemáticas, los estudiantes con discapacidades de aprendizaje en matemáticas no suelen seguir usando esta estrategia para solucionar problemas por cuenta propia.
La investigación indica
- Los estudiantes que usan las representaciones visuales precisas tienen seis veces más probabilidades de resolver problemas de matemáticas correctamente que los estudiantes que no las usan. Sin embargo, los estudiantes que usan las representaciones visuales de forma imprecisa tienen menos probabilidades de resolver problemas de matemáticas correctamente que los que no usan representaciones visuales.
(Boonen, van Wesel, Jolles, & van der Schoot, 2014) - Los estudiantes con discapacidades de aprendizaje no suelen hacer representaciones visuales precisas ni las usan de forma estratégica para resolver problemas. Enseñarle a los estudiantes a usar representaciones visuales sistemáticamente para resolver problemas verbales ha llevado a mejoras significativas en el rendimiento de matemáticas de los estudiantes con discapacidades de aprendizaje.
(van Garderen, Scheuermann, & Jackson, 2012; van Garderen, Scheuermann, & Poch, 2014) - Los estudiantes que usan representaciones visuales para resolver problemas verbales tienen más probabilidades de resolver los problemas correctamente. Lo mismo ocurrió con los estudiantes que tenía discapacidades de aprendizaje, que tenían bajo rendimiento, o que tenían rendimiento promedio.
(Krawec, 2014)
Las representaciones visuales son flexibles; se pueden usar en todos los grados y tipos de problemas de matemáticas. Pueden ser usados por maestros para enseñar hechos de matemáticas y por estudiantes para aprender contenido matemático. Las representaciones visuales pueden tener múltiples formas. Haga clic en los enlaces a continuación para ver algunas de las representaciones visuales más comunes usadas por maestros y estudiantes.
¿Cómo se alinea esta práctica?
Prácticas de alto rendimiento (HLP, por sus siglas en inglés)
- HLP15: Proporcionar apoyos estructurados (scaffolded)
Estándares Comunes Estatales de Matemáticas (CCSSM): Estándares para la práctica de matemática
- MP1: Interpretar los problemas y perseverar en resolverlos.
Definición: Una línea recta que muestra el orden de y la relación entre números.
Usos comunes: sumar, restar, contar
Definición: Una barra dividida en rectángulos que representa con precisión las cantidades indicadas en el problema.
Usos comunes: sumar, fracciones, proporciones, razones
Definición: Dibujos simples de objetos reales y concretos (p. ej., canicas, camiones).
Usos comunes: contar, sumar, restar, multiplicar, dividir
Definición: Dibujos que ilustran información usando líneas, figuras y colores.
Usos comunes: comparar números, estadísticas, razones, álgebra
Definición: Material visual que ayuda a los estudiantes a recordar y organizar información, así como ilustra las relaciones entre ideas (p. ej., redes de palabras, tablas, diagramas de Venn).
Usos comunes: álgebra, geometría
| Triángulos | ||
|---|---|---|
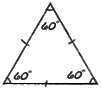
| equilátero | -todos los lados son iguales -todos los ángulos son de 60° |
 |
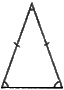
| isósceles | -dos lados son iguales -dos ángulos son iguales |
 |
| escaleno | -ningún lado es igual -ningún ángulo es igual |
 |
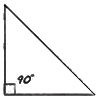
| rectángulo | -un ángulo es de 90° (ángulo recto) -el lado opuesto al ángulo recto es el lado más largo (hipotenusa) |
 |
| obtuso | -un ángulo es mayor de 90° |  |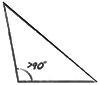
| agudo | -todos los ángulos son menor de 90° |  |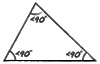
No obstante, antes de que los estudiantes puedan resolver los problemas, los estudiantes deben saber antes qué tipo de representación visual crear y usar para determinado problema de matemáticas. Algunos estudiantes—los estudiantes de alto rendimiento y los estudiantes talentosos específicamente—hacen esto automáticamente, mientras que otros necesitan que se les explique cómo hacerlo de forma explícita. Esto es el caso de los estudiantes que tienen dificultades con las matemáticas especialmente y los que tienen discapacidades de aprendizaje matemáticas. Sin instrucción explícita, sistemática sobre cómo crear y usar representaciones visuales, estos estudiantes suelen crear representaciones visuales que son desorganizadas o que contienen información incorrecta o parcial. Considere los ejemplos a continuación.
Ejemplo de escuela primaria
La Sra. Aldridge le pide a sus estudiantes de primer grado que sumen 2 + 4 haciendo dibujos de puntos.
Talia dibuja lo siguiente:
Colby dibuja lo siguiente: 
Note usted que Talia llega a la respuesta correcta. Sin embargo, como Colby dibuja sus puntos desordenadamente, no consigue contarlos todos y, por consiguiente, llega a la respuesta incorrecta.
Ejemplo de escuela secundaria
El Sr. Huang le pide a sus estudiantes que resuelvan el siguiente problema verbal:
El mástil de la bandera debe ser reemplazado. La escuela quiere reemplazarlo con un mástil del mismo tamaño. Cuando Juan está parado a 11 pies de la base del mástil, el ángulo de elevación desde los pies de Juan a la cima del mástil es de 70 . ¿De qué altura es el mástil?
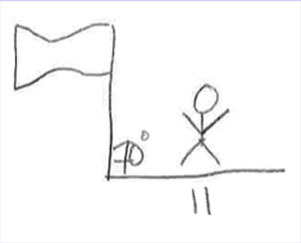
Compare el dibujo a continuación creado por Brody y Zoe para representar este problema. Note que Brody dibujó una representación precisa y aplicó la estrategia correcta. En cambio, Zoe hizo un dibujo con información parcialmente correcta. El número 11 está en el lugar correcto, pero el 70° no lo está. Como consecuencia de su representación imprecisa, Zoe es incapaz de seguir adelante y resolver el problema. Sin embargo, en el caso de recibir una representación más precisa desarrollada por otra persona, Zoe tendría más probabilidades de solucionar el problema correctamente.
Brody
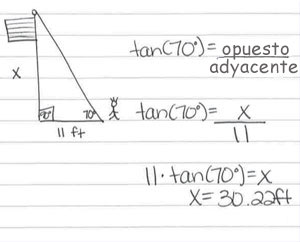
Zoe
Materiales manipulativos
Algunos estudiantes no podrán comprender destrezas y conceptos de matemáticas usando los tipos de representaciones mostrados en la tabla arriba solamente. Niños muy jóvenes y estudiantes que tienen dificultades con las matemáticas suelen requerir diferentes tipos de representaciones visuales que se conocen como manipulativos. Estos materiales y objetos, concretos y prácticos—un ábaco o monedas, por ejemplo—ayudan a los estudiantes a representar la idea matemática que están tratando de aprender o el problema que están tratando de solucionar. Los materiales manipulativos pueden ayudar a los estudiantes a desarrollar un entendimiento conceptual de temas de matemáticas. (En este módulo, el término objetos concretos se refiere a manipulativos y el término representaciones visuales se refiere a diagramas esquemáticos.)
Es importante que el maestro haga conexiones explícitas entre el objeto concreto y el concepto abstracto que se está enseñando. La meta es que el estudiante eventualmente entienda los conceptos y procedimientos sin la necesidad de usar manipulativos. En el caso de los estudiantes de escuela secundaria que tienen dificultades con las matemáticas, los maestros deben enseñar la parte abstracta junto a la representación concreta o visual y establecer una conexión explícita entre ambos.
Una transición de objetos concretos o representaciones visuales a ecuaciones abstractas puede ser difícil para algunos estudiantes. Una estrategia que los maestros pueden usar para ayudar a los estudiantes a hacer una transición más sistemática entre los objetos concretos, las representaciones visuales, y las ecuaciones abstractas es el marco de referencia Concreto-Representativo-Abstracto (CRA, por sus siglas en inglés).
Marco Concreto-Representativo-Abstracto
El marco de referencia Concreto-Representativo-Abstracto (CRA, por sus siglas en inglés) ayuda a los estudiantes a ganar comprensión conceptual de un proceso de matemáticas, en vez de simplemente completar el algoritmo (p.ej., 2 + 4, 2x + y = 27). Conectar objetos concretos y representaciones visuales de forma sistemática es una forma de estructurar y dar soporte a la comprensión de un estudiante. Los componentes de este marco de referencia son:
- Concreto—Los estudiantes interactúan y manipulan objetos tridimensionales, azulejos de álgebra u otros manipulativos de álgebra con representaciones de variables o unidades.
- Representativo—Los estudiantes usan dibujos bidimensionales para representar problemas. Estas imágenes pueden ser presentadas por sus maestros, o por medio del currículo usado en el salón de clase, o los estudiantes pueden dibujar su propia representación del problema.
- Abstracto—Los estudiantes solucionan problemas con números, símbolos y palabras sin asistencia concreta o representativa alguna.
El marco de referencia Concreto-Representativo-Abstracto es efectivo para todas las edades y puede ayudar a los estudiantes a aprender conceptos, procedimientos, y aplicaciones. Cuando se implementa cada uno de los componentes, los maestros deben usar instrucción explícita, sistemática y monitorear el trabajo de los estudiantes regularmente para evaluar su comprensión, haciéndoles preguntas sobre su proceso de pensamiento y proporcionando clarificaciones según sea necesario. Las actividades concretas y representativas deben reflejar el proceso real de la solución del problema para que los estudiantes puedan generalizar el proceso de resolver una ecuación abstracta. La ilustración a continuación destaca cada uno de estos componentes.
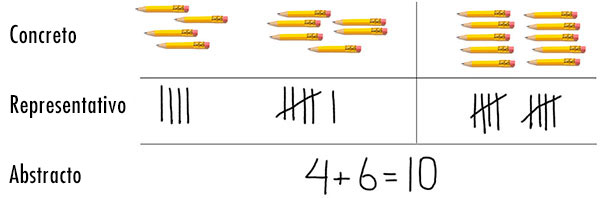
Para su información
La estrategia CRA-I (Concreto-Representativo-Abstracto) es una práctica prometedora que ayuda a mover a los estudiantes de secundaria con dificultades en matemáticas o discapacidades del uso de materiales manipulativos y representaciones visuales a la ecuación abstracta rápidamente. En esta versión modificada de CRA, el maestro presenta el contenido usando objetos concretos, representaciones visuales de objetos concretos, y la ecuación abstracta de forma simultánea. Los estudios muestran que este marco de referencia es efectivo para la enseñanza de álgebra a esta población de estudiantes (Strickland & Maccini, 2012; Strickland & Maccini, 2013; Strickland, 2017).
Kim Paulsen discute los beneficios de los materiales manipulativos y otras cosas que tener en cuenta cuando se están usando (tiempo: 2:35).
Kim Paulsen, EdD
Profesora Asociada, Educación Especial
Universidad de Vanderbilt
Transcripción: Kim Paulsen, EdD
Los materiales manipulativos son una gran manera de ayudar a los niños a entender conceptualmente. El uso de materiales manipulativos realmente ayuda a los estudiantes a ver las cosas conceptualmente, y los ayuda a entender. Algunas de los cosas, no obstante, que debemos recordar cuando estamos usando materiales manipulativos es que es importante darle a los estudiantes un poco de tiempo libre cuando están usando un material manipulativo nuevo para que puedan explorar con material. Es importante que tengamos reglas específicas de cómo usar los manipulativos, que no son juguetes, que en realidad son materiales de aprendizaje, y cómo los estudiantes deben tomarlos, cómo deben guardarlos, cuál es la hora apropiada para usarlos, y asegurarnos de que no son distractores mientras hacemos la presentación de parte de la lección. Algo importante es que no queremos que los estudiantes se memoricen el algoritmo o los procedimientos mientras estén usando los materiales manipulativos. En realidad trata de ayudarlos a entender conceptualmente. Eso no quiere decir que los estudiantes van a entender conceptualmente automáticamente o que van a poder pasar del uso de materiales manipulativos a solucionar problemas. Para algunos niños, es difícil usar los materiales manipulativos. No es así como aprenden, así que no los forzamos a usar materiales manipulativos si no es algo útil para ellos. Así que tenemos que recordar que los materiales manipulativos son una forma de pensar en la enseñanza de matemáticas.
En parte creo que algunos maestros no usan estos materiales porque toma mucho tiempo, mucha organización, y porque también sienten que los estudiantes se vuelven muy dependientes del uso de materiales manipulativos. Una forma de pensar en el uso de los materiales manipulativos es que los usas durante un par de clases cuando estás enseñando un concepto nuevo, y luego los retiras para que los estudiantes puedan hacer el cálculo solamente. Es cierto que no podemos andar por la vida con materiales manipulativos en las manos. Y me parece que otra de las razones de porqué muchas escuelas o maestros no usan manipulativos es porque son muy costosos. Por lo tanto, sería muy útil si todos los maestros en la escuela pudieran reunir recursos y tener un salón con materiales manipulativos donde los maestros puedan ir y ver los materiales para que no sea tan costosos. Los maestros tienen que saber cómo usarlos, y eso toma mucha práctica.
