How can teachers determine whether students are making appropriate progress?
Page 3: Select a Measure
 The first step in the progress monitoring process is to select a measure. Recall that these measures should include sample items for all skills across the entire academic year. Often, the mathematics program selected by the school or district will include grade-level progress monitoring measures. In other instances, specific GOM measures might be chosen by school, district, or state administrators. This is typically the case when a school is using an MTSS or RTI framework for instruction. Educators can also decide independently to use GOM measures to monitor student progress and make instructional decisions. Regardless of who is making the choice, it’s important to keep several factors in mind when selecting a GOM measure:
The first step in the progress monitoring process is to select a measure. Recall that these measures should include sample items for all skills across the entire academic year. Often, the mathematics program selected by the school or district will include grade-level progress monitoring measures. In other instances, specific GOM measures might be chosen by school, district, or state administrators. This is typically the case when a school is using an MTSS or RTI framework for instruction. Educators can also decide independently to use GOM measures to monitor student progress and make instructional decisions. Regardless of who is making the choice, it’s important to keep several factors in mind when selecting a GOM measure:
- Does it align with the grade-level mathematics skills?
- Is the measure reliable and valid?
- Does the measure have sufficient alternate versions?
- Is the measure relatively quick (e.g., two to ten minutes) and easy to administer?
- Is the measure designed to be administered to individual students or to groups? (Group-administered tests are often more convenient than individually administered ones.)
- Are versions of the test available in languages other than English?
For the earlier grade levels (e.g., kindergarten, first grade), educators will most likely need to assess early numeracy skills, such as number identification. However, for students who have mastered these basic skills, the educator can administer two other types of mathematics probes: computation probes and concepts and applications probes.
| Computation Probe | Concepts and Applications Probe* | |
| Measures students’ procedural knowledge (e.g., ability to add fractions). | Assesses conceptual understanding of mathematics or students’ ability to apply mathematics knowledge (e.g., to make change from a purchase). | |
|
|
|
|
|
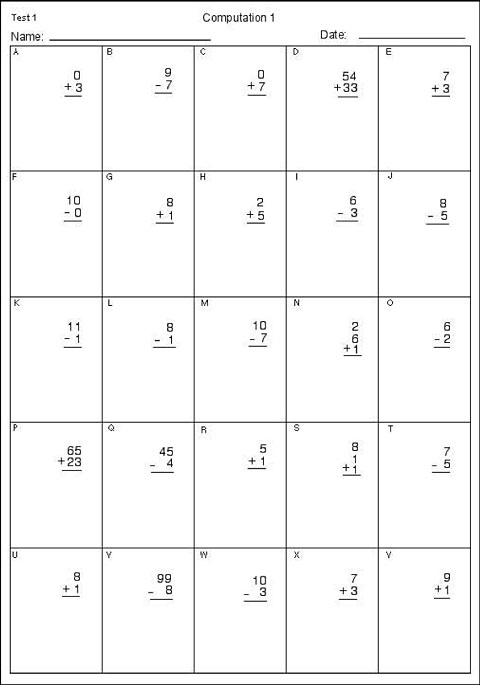
Sample Elementary Computation Probe This probe is a white sheet of paper with spaces to fill in the student’s name and date across the top of the page. In the upper right-hand corner, the page is labeled “Test 1.” Underneath the name and date, the page is titled in the center “Computation.” The page is divided into five columns and five rows, with each computation problem labeled with a letter of the alphabet. The computation problems are adding two or three single-digit numbers, adding two two-digit numbers without regrouping, subtracting two single-digit numbers without regrouping, and subtracting a single-digit number from a two-digit number. The sample secondary algebra probe below is designed to assess students’ basic algebraic skills. Note that a normal probe would contain 60 questions and allow students five minutes to complete them.This 30-item example, which is the first of a two-page probe, is presented here for the sake of brevity and illustrative purposes.
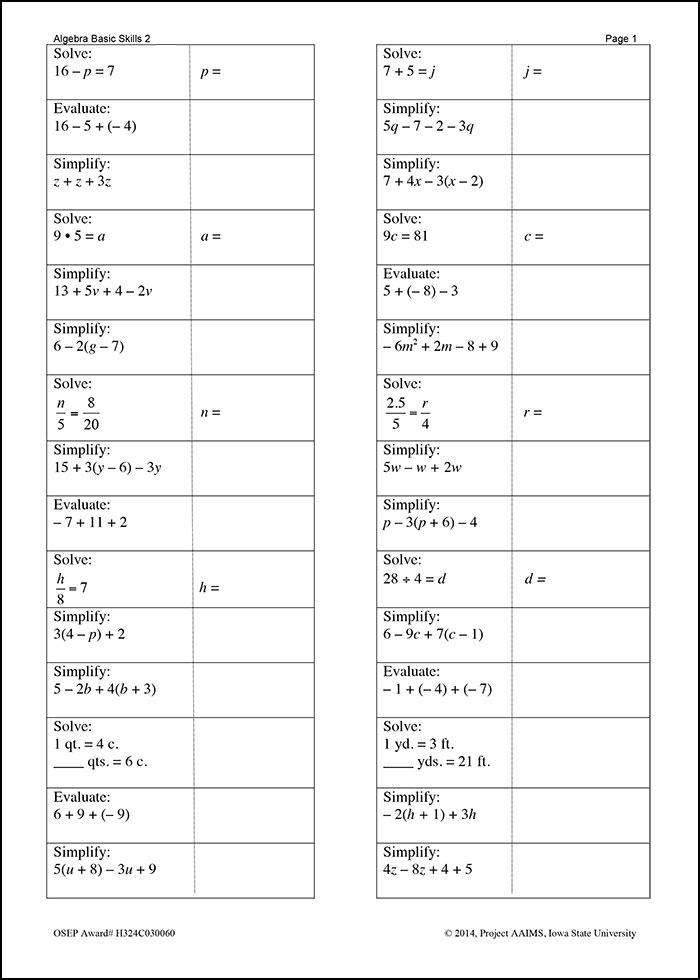
Project AAIMS. (2014). Project AAIMS algebra progress monitoring measures [Algebra Basic Skills, Algebra Foundations]. Ames, IA: Iowa State University, College of Human Sciences, School of Education, Project AAIMS. Sample Secondary Algebra Probe This sample secondary algebra probe is a single sheet featuring 30 mathematics problems. The questions ask students to solve simple equations (e.g., 16 minus p equals 7, p equals), use the distributive property [e.g., 16 minus 5 plus (negative 4)] , compute with integers (e.g., 9 times 5 equals a), combine like terms (13 plus 5v plus 4 minus 2v), and use proportional reasoning (n over 5 equals 8 over 20, n equals). The top of the sheet is labeled “Algebra Basic Skills 2, Page 1.” Note that this is the first of a two-page computation probe containing 60 questions.
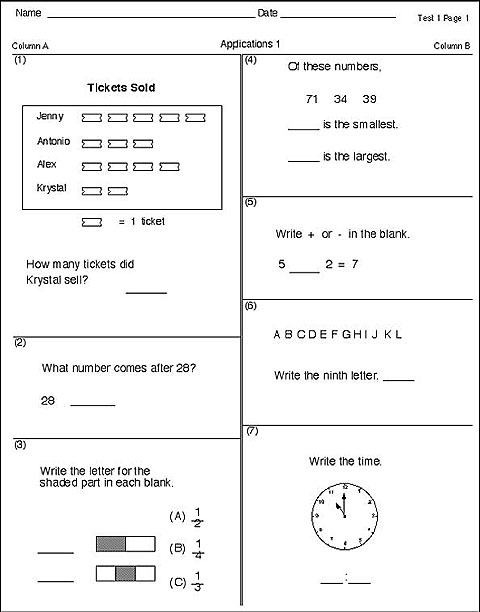
Sample Elementary Concepts and Applications Probe This graphic is of a sample concepts and applications probe. It is a white sheet of paper with spaces to fill in your name and date across the top of the page. In the upper right-hand corner the page is labeled, “Test 1 Page 1.” Underneath the name and date the page is titled in the center “Applications 1.” The page is divided into two columns, column A labeled on the left and column B labeled on the right. Column A is divided into three uneven rectangles to delineate questions 1 through 3. Question 1 shows the title, Tickets Sold, with a picture graph below. Four names are listed—Jenny, Antonio, and Alex, Krystal—with variable pictures of tickets lined up beside their names. Underneath the names is a key, showing a picture of one ticket as equal to 1 ticket. Below the picture graph is the question: How many tickets did Krystal sell?, with a space to put an answer. There is a dividing line before question 2. Question 2 asks “What number comes after 29?” Below the question is the number 29 with a space to the right of the number to place an answer. There is another dividing line before question 3. Question 3 states “Write the letter for the shaded part in each blank.” Two blanks are provided, one on top of the other. To the right of each blank is a rectangle that is partly shaded. To the right of the shaded rectangles are three answer choices, one on top of the other. Answer choice A is 1/2, answer choice B is 1/4, and answer choice C is 1/3. Column B is divided into four uneven rectangles to delineate questions 4 through 7. Question 4 has the beginning phrase “Of these numbers…” then the numbers 71, 34, and 39 written below. Below the numbers is a blank then the text “is the smallest?” Below that statement is another blank and the text “is the largest?” There is a dividing line and then question 5 which states “Write + or – in the blank.” Below the text is the following incomplete number sentence: 5_____2 = 7. Question 6 begins under another dividing line and lists the alphabet letters ABCDEFGHIJKL. Below the letters is the statement “Write the ninth letter” with a blank to the right of the statement to fill in an answer. The last question, question 7, begins after the dividing line. It states “Write the time.” There is a picture of a clock with the hour hand pointing to the 10 and the minute hand pointing to the 12. Below the clock is a blank, then a colon, and another blank to record the time on the clock. |
||
* No valid middle or high school concepts and applications probes are available at this time.
When selecting a progress monitoring measure, educators should consider the student’s long-term goal (i.e., the skills they want their student to master by the end of the year). If the student is expected to master computation skills by the end of the year, the educator should administer computation probes. However, if the student is performing well with computation skills, and instead is expected to master concepts and application skills by the end of the year, the educator can administer concepts and applications probes in addition to or instead of computation probes.
For Your Information
Though a variety of GOM measures are commercially available in mathematics for grades K through 12, tests for secondary students are limited. These standardized measures typically include the tests, administration procedures, and scoring guides that have been developed to produce reliable and valid scores. Additionally, student benchmarks and the expected rate of improvement (ROI) are often provided by the developer.
standardized measure
Test, measure, or probe in which all test takers are asked to answer the same questions (or alternate but equivalent questions) and which are subsequently scored in a uniform manner so as to permit a relative comparison of student performance.
 The National Center on Intensive Intervention (NCII) provides a tools chart that presents information about commercially available progress monitoring probes that have been reviewed by a panel of experts and rated on key features.
The National Center on Intensive Intervention (NCII) provides a tools chart that presents information about commercially available progress monitoring probes that have been reviewed by a panel of experts and rated on key features.
For information about conceptual and procedural measures for algebra, including sample forms, visit the Algebra Screening & Progress Monitoring project website.
There is a lack of available validated progress monitoring measures to assess the mathematics skills of high school students. This is especially true of measures that assess students’ conceptual understanding. For this reason, educators may want to use qualitative measures, such as diagnostic interviews or work sample measures. Although these types of assessments are not viable methods for progress monitoring, they can help educators understand how students develop their mathematical thinking. David Allsopp discusses the benefit of using diagnostic interviews to assess students’ conceptual understanding (time: 1:56).

David Allsopp, PhD
Assistant Dean for Education and Partnerships
University of South Florida
Transcript: David Allsopp, PhD
I think we need to be looking at ways to more qualitatively understand how kids are developing their mathematical thinking. One is really having measurement tools that get at the complexity and the importance of mathematical thinking. The reality is that being able to quickly evaluate where students are from a progress monitoring perspective, there’s always going to be this focus mostly on procedural knowledge. Are we also going to evaluate conceptual understanding? They’re not separate entities. They’re important, both of them, to assess.
On the other hand, I think there definitely are formative and informal assessment options that can be really powerful for educators to really get at what students are thinking, what they’re understanding. One is diagnostic interviews, where students talk through what they did and why they did it in terms of problem-solving. And as you’re listening, what students are saying and the extent to which they have misconceptions or if they are applying a concept incorrectly or if they have a procedure mixed up, this is a way that educators can better understand where kids are in terms of their thinking about a particular application or procedure or problem-solving context so that they can better target their intervention to address those areas. If we just are looking at student’s responses and whether they’re right or wrong, we don’t necessarily have a very good understanding of why it’s right or wrong. That’s a really important component to being able to really, precisely intervene with kids when they’re struggling in mathematics.
Grade level GOM measures are appropriate for typically achieving students as well as for many who are struggling. However, these measures might not be appropriate for students who are consistently not performing at grade level. These students might require a measure designed for a different grade level. Sometimes, commercially available measures include directions on selecting an appropriate grade-level probe for these students. If they do not, however, educators should:
Example
Although Sam is a fourth-grade student, he has mathematics difficulties and performs below grade level. To select an appropriate CBM measure, his teacher:
- Administers three third-grade level probes—the grade level probe that includes the math skills Sam is expected to master by the end of the year.
- Identifies Sam’s median score. Because Sam’s median score is 12, the teacher feels confident that the third-grade level probe is appropriate for progress monitoring.
- Continues to administer third-grade level probes for the rest of the year.
- Administer three computation probes at the grade level the student is expected to perform by the end of the year. Recall that this may not be the student’s current grade level. Additionally, keep in mind that educators may want to administer concepts and applications probes in addition to or instead of computation probes if the student is doing well in computation but struggling with problem-solving.
- Identify the student’s median score for the three probes. Use the chart below to select the appropriate grade-level probe. As indicated in the table, the educator might need to administer additional probes at higher and lower levels until the correct grade-level probe is identified.
x
median
The middle value found by ordering scores from lowest to highest.
| Digits/Blanks Correct | Rules for Selecting an Appropriate-Level Measure |
| <10 | Move down one grade level and repeat procedure. |
| 10-15 | Use the identified probe. |
| >15 | Move up one grade level and repeat procedure, but do not exceed the student’s current grade level. |
- Monitor the student’s progress using probes at the determined goal level throughout the entire school year.