How can teachers determine whether students are making appropriate progress?
Page 6: Administer, Score, and Graph
After preparing a graph for each student, now the educator is ready to administer and score GOM reading measures. The educator should take care to ensure fidelity of implementation by following any accompanying guidelines for the measure. After administering and scoring each probe, the educator should graph each student’s scores to create a visual representation of his performance over time. Read on to learn more about this process.
fidelity of implementation
The degree to which an intervention is implemented accurately, following the guidelines or restrictions of its developers.
Administer Measures
For Your Information
To monitor the progress of struggling students, educators should administer measures weekly or twice weekly. More frequent monitoring enables educators to make decisions and adjust instruction, if needed, more quickly.
The educator should administer the selected progress monitoring measure frequently and at regular intervals. Although some commercially available measures are designed to be used once or twice per week, others are designed to be used once or twice per month. (Some commercially available measures indicate how frequently the measure should be administered.) At a minimum, though, progress monitoring measures should be administered once per month. Mathematics measures can be administered in a variety of ways. These include:
- Individually — Educators administer measures to individual students; this might be required for any grade level but is almost always the case for early numeracy skills (e.g., oral counting, number identification).
- In groups — Educators administer measures to the entire class at the same time.
- Using a computer — Students individually complete the measures on a computer.
Regardless of how they are administered, the students should try to complete as many problems or questions as possible during the allotted time, typically between two to ten minutes, depending on the grade level and the type of measure.
Tips for Administering Probes
- Explain to students that although they may not get a lot of correct answers on the probes at first, as the year progresses and as they learn new skills, their performance will continue to improve.
- Establish consistent administration procedures. Doing so facilitates the comparison of student performance over time and helps confirm that their scores are accurate reflections of their ability and not the result of inconsistent administration.
- Administer probes at the same time of day. If using both computation probes and concept and application probes, administer one after another and in the same order.
- If possible, avoid increasing the allotted probe completion time for students with disabilities whose IEPs specify testing accommodations because this prevents the comparison of student scores to national norms. When time increases are necessary, provide the same amount of time each time a probe is administered.
In the video below, an educator individually administers a number identification measure. Notice how the educator provides precise directions, carefully following the administration guidelines associated with that measure to ensure implementation fidelity and accurate measurement (time: 1:43).
Source: National Center on Intensive Intervention
Score Measures
Commercially available probes include detailed standardized procedures to produce reliable and valid scores. Failing to follow these procedures can lead to inaccurate and misleading conclusions. In general, scoring a computation or a concepts and applications probe is a matter of determining how many items the student has solved correctly. However, depending on the grade level of the students, some additional scoring options might be available.
Elementary: In the case of elementary students, educators have the additional option of scoring computation probes according to the number of digits correct. Regardless of whether they score by problems correct or digits correct, educators in all classes and grades at a given school should score probes in the same way so that the scores are comparable. In the link below, there is an example of an elementary computation probe that has been scored using both number of digits correct and number of problems correct.
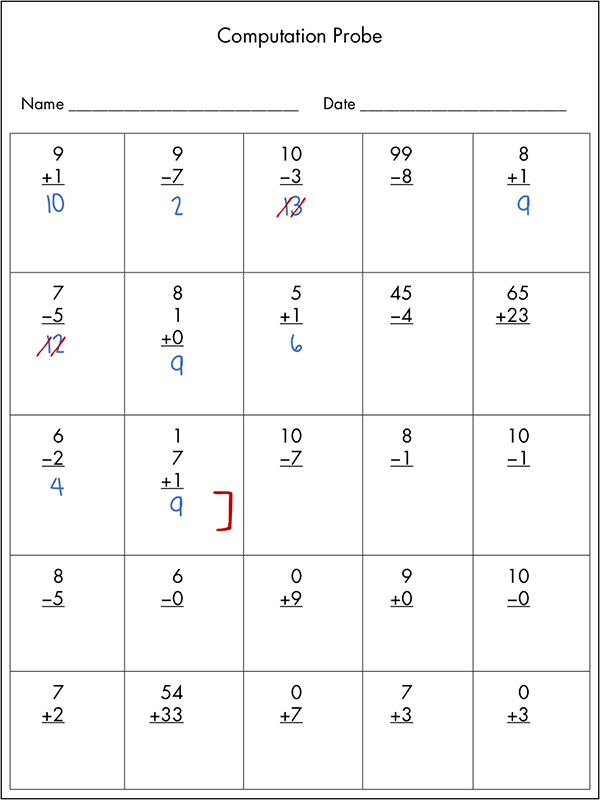
The following elementary computation probe has been scored using two different methods:
- Number of digits correct — The teacher placed a green dot under each correct digit and a red slash through each incorrect digit.
- Number of problems correct — The teacher placed a “C” next to each correct problem.
This probe is a white sheet of paper with spaces to fill in the student’s name and date across the top of the page. In the upper right-hand corner, the page is labeled “Test 1.” Underneath the name and date, the page is titled in the center “Computation.” The page is divided into five columns and five rows, with each computation problem labeled with a letter of the alphabet. The computation problems are adding two or three single-digit numbers, adding two two-digit numbers without regrouping, subtracting two single-digit numbers without regrouping, and subtracting a single-digit number from a two-digit number.
Secondary: For students in middle and high school, problems should be scored by the number of problems correct. In the case of multi-step problems, partial credit can be given for correctly performed steps. Click the link below for an example of a scored secondary computation probe.
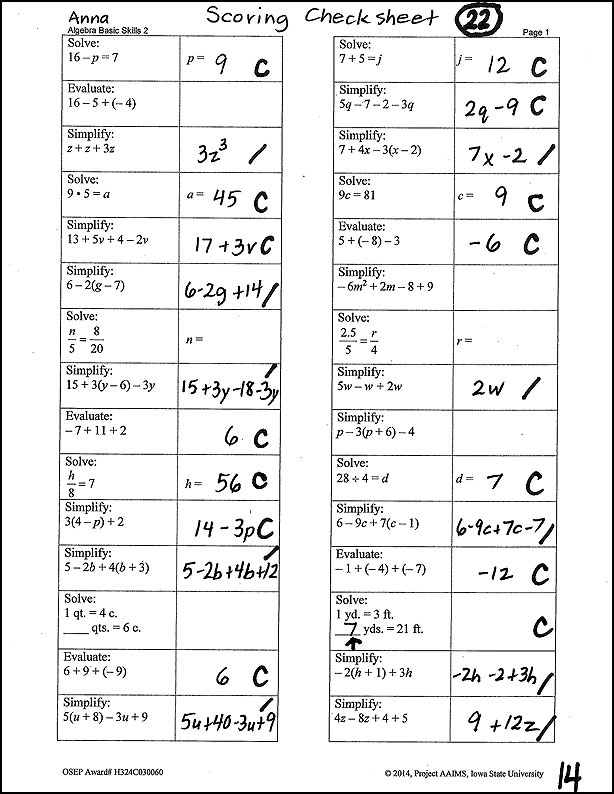
The sample secondary computation probe below is designed to assess students’ basic algebraic skills. Note that a normal probe would contain 60 questions and allow students five minutes to complete them. This 30-item example, which is the first of a two-page probe, is presented here for the sake of brevity and illustrative purposes. Anna has taken this probe and scored 22 problems correct out of 60. The 14 in the bottom right-hand corner of the sheet indicates the number Anna completed correctly out of this page’s 30 questions. To grade the probe, her teacher follows the standard scoring rules:
- Ignore skipped problems
- Accept mathematically equivalent answers
- Mark correct answers with a “C”
- Mark incorrect answers with a slash (/)
Anna’s final score on the probe is the number of questions she answered correctly.
Project AAIMS. (2014). Project AAIMS algebra progress monitoring measures [Algebra Basic Skills, Algebra Foundations]. Ames, IA: Iowa State University, College of Human Sciences, School of Education, Project AAIMS.
This sample secondary computation probe is a single sheet featuring 30 mathematics problems.The questions ask students to solve simple equations (e.g., 16 minus p equals 7, p equals), use the distributive property [e.g., 16 minus 5 plus (negative 4)] , compute with integers (e.g., 9 times 5 equals a), combine like terms (13 plus 5v plus 4 minus 2v), and use proportional reasoning (n over 5 equals 8 over 20, n equals). The top of the sheet is labeled “Algebra Basic Skills 2, Page 1.” This is Anna’s probe. Her name is written in the top left-hand corner next to the words “Scoring Check Sheet.” Near the top right-hand corner, the number 22 is circled. This indicates the total number of problems that Anna answered correctly out of 60, and therefore her final score. In the bottom right-hand corner is the number 14, indicating the number of problems Anna worked correctly out of the 30 items on this page. Her teacher has scored the probe by marking 14 correct answers with a “C” and 10 incorrect ones with a slash mark. She has 6 skipped problems that Anna did not attempt to answer.
Although scoring probes using digits correct is a viable option at the elementary level, it is not recommended at the secondary level. Lynn Fuchs points out several issues that school personnel should consider as they decide whether to score probes by the number of digits correct or the number of problems correct (time: 1:05). Next, Brad Witzel discusses the reasoning behind giving partial credit for correctly performed steps in multi-step problems (time: 1:04).
Lynn Fuchs, PhD
Dunn Family Chair in Psychoeducational Assessment
Department of Special Education
Vanderbilt University
Transcript: Lynn Fuchs, PhD
Scoring by digits correct only applies to computation problems, not most other forms of math skill. If we score computation probes in terms of problems correct, it can be more difficult to see small amounts of improvement. It’s like having a scale for measuring your weight which only will show you five-pound intervals, so it would take you a long time to see the effects of your diet.
There is a disadvantage in scoring digits, though, because it requires more skill and training to be able to do the scoring. It can also take more time to score digits correct than to score problems correct. And, of course, accuracy is very important, and a school has to make a determination about how they can ensure scoring accuracy if they are using digits correct.
Transcript: Brad Witzel, PhD
I have some caution in digits-correct versus incorrect. I propose that we assess middle school- and high school-level probes through a procedural facility. So think, What are the reasonable steps that a student must know in order to solve an equation accurately? Then we assess the student based on their approach, along with reasoning of that approach. When we grade by steps, in tackling a multi-step complex problem, you’re able to determine not only if the answer is correct but how the student accomplished their goal. More importantly, if the student’s answer is incorrect, you won’t just say the problem’s wrong, the student needs to learn the whole process again. That’s not true.
If you grade it by these incremental steps, you’ll be able to determine why the problem was incorrect and then set up a targeted intervention to help that student with that one error. This approach allows you to identify procedural misunderstandings and even set up a follow-up interview to reveal their reasoning issues as well.
Graph Scores
Activity
Ms. Wu has been administering computation probes to her students for the last four weeks. Recall that Raymond is taking a first-grade test because he is performing far below grade level. Raymond’s most recent computation test (Week 6) is below. Score this test for digits correct. Enter your answer below:
Correct
Now on the graph below, plot Raymond’s last four weeks of computation scores (Week 3-6). Ms. Wu administers the probes on Tuesdays, so be sure to plot the data on the correct day. The box below contains Raymond’s data for Weeks 3-5: 8, 9, 9. The test you scored should be entered for Week 6.
- Week 3=8
- Week 4=9
- Week 5=9
- Week 6=?
