How can teachers determine whether students are making appropriate progress?
Page 5: Create a Goal Line
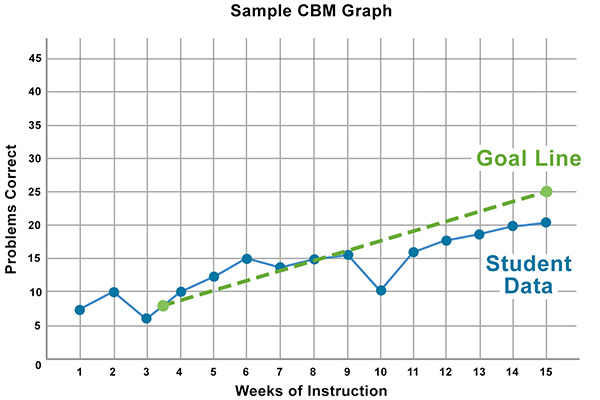To more quickly evaluate a student’s performance over time, the teacher will find it helpful to add a goal line to the student’s graph. The goal line represents the progress a student is expected to make throughout the year. It is simply a line on the graph that connects an individual student’s baseline performance to her expected mid-year or end-of-year performance goal. Creating a goal line involves establishing a baseline and determining the expected goal. Let’s examine each of these steps in detail.
Establish a Baseline
To create a goal line for each student, the teacher must first determine each student’s baseline—or current level of performance. A stable, clear baseline can usually be established with three to five data points collected over a short span (e.g., three consecutive days). Once the data are collected, the teacher should identify the median score—the score that falls in the middle when scores are ordered from lowest to highest. This score is then plotted on the student’s graph.
Example: A student receives scores of 7, 5, and 8 on three consecutive days. To determine the median the teacher orders the scores from lowest to highest and then chooses the one in the middle: 5 7 8. The median is 7.
Determine the Expected Goal
Once an educator has established the baseline, she can next determine and plot the expected goal. When doing so, it’s important that the teacher set ambitious long-term goals for every student. Most commercially available GOM measures include mid-year and end-of-year (EOY) performance benchmarks or goals that are based on national norms. These can be used for typically developing students as well as for those at-risk. For example, the benchmarks below are for the Vanderbilt Computation and Concepts and Applications measures.
| Grade | Computation | Concepts and Applications |
|---|---|---|
| Kindergarten | N/A | N/A |
| 1st | 20 digits | 20 points |
| 2nd | 20 digits | 20 points |
| 3rd | 30 digits | 30 points |
| 4th | 40 digits | 30 points |
| 5th | 30 digits | 15 points |
| 6th | 35 digits | 15 points |
Draw the Goal Line
Now that the student’s baseline and goal have been plotted, the next step is to draw a line between these two points. This is the goal line. (Note that, just as students’ median baseline data points will vary, so too will the placement of the goal line differ from student to student.) The goal line represents the student’s expected average weekly rate of growth or rate of improvement (ROI) needed to meet her end-of-year goal. For example, an ROI of 3 means that the student would need to correctly solve three additional problems correctly per week to stay on track to meet the end-of-year goal. Most commercially available GOM measures include the ROI.
Once a student’s data have been plotted on the graph, the teacher can determine whether the student is on target to reach the identified goal within the established timeframe. This is a quick and simple process that involves comparing the student’s data in relation to the goal line.
For Your Information
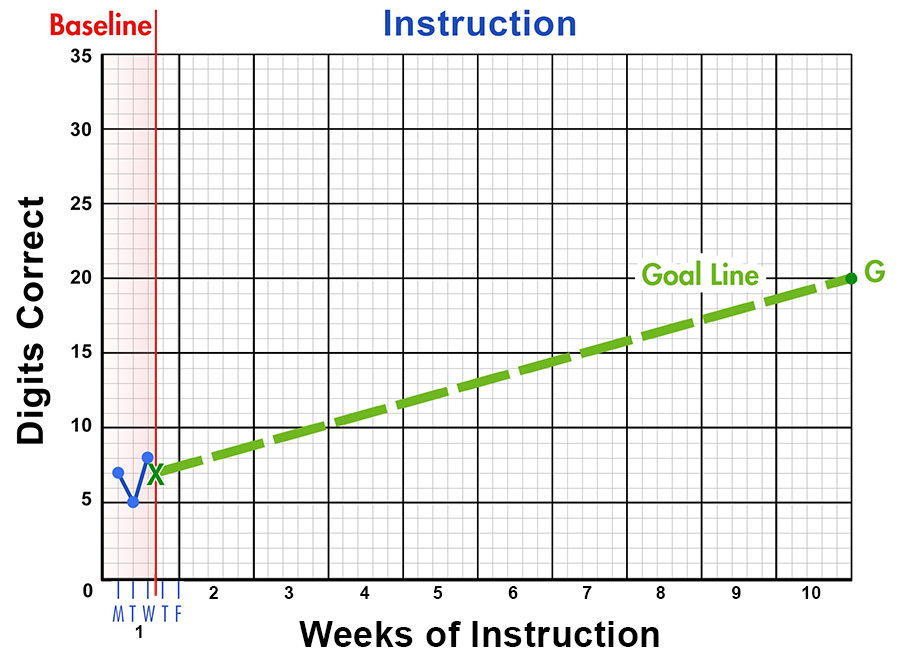
In addition to creating a long-term goal, the teacher might want to create a short-term goal to help motivate students to maintain their efforts or improve their performance. Once a goal line has been added to the graph, an educator can set a short-term (e.g., weekly, monthly) goal for a student relatively easily. For example, look at the sample graph below. If the educator wanted to establish a nine-week goal for this student, she would find the nine-week mark on the horizontal axis and follow it up to the goal line. She would then identify which score aligns with that point on the vertical axis to find the nine-week goal. In the example graph below, the nine-week goal for this student is to correctly solve 32.5 problems.
Activity
Lana is a student in Ms. Wu’s second-grade class. Using the provided data, answer each of the questions below and plot Lana’s goal line on the graph.
|
|
|
|
|
|
Determining Goals for Struggling Students
Students whose performance is significantly below grade level often require an end-of-the-year goal based on their individual ROI rather than the goals for typically achieving students. Because these students are often receiving services provided by an interventionist or special education teacher, these professionals might provide support for general education teachers when developing such individual goals. They can do this by using the intra-individual framework described below.
| Step | Actions | Example |
|
Gather scores |
Gather the eight most recent test scores. |
Colby’s eight most recent test scores: |
| Determine median test score |
Subtract the median of the 1st three test scores from the median of the last three test scores. |
9, 12, 14, 11, 15, 14, 12, 15 Median of first three test scores (9, 12, 14) 14 – 12 = 2 |
| Find current rate of improvement (ROI) |
|
Student’s current ROI =.29 |
|
Determine expected ROI |
Multiply the student’s current ROI by 1.5 to get the student’s expected ROI. To close the achievement gap, the student needs to make fifty percent more progress than what they are currently making. Therefore, multiply ROI by 1.5. |
Student’s current ROI x 1.5 .29 x 1.5=.44 Expected ROI=.44 |
|
Determine amount of growth needed |
Multiply the expected ROI by the number of weeks remaining in the school year to determine the amount of growth the student needs to reach the end of the school year. |
Expected ROI=.44 Number of weeks remaining=28 .44 x 28 = 12 By the end of the school year, Colby’s performance should improve by 12 problems correct. |
|
Calculate baseline score |
Calculate the student’s baseline score by finding the mean (average) of the three most recent data points. |
Colby’s first 8 data points: (14+12+15)/3= 14 |
|
Identify end-of-year goal |
Add the student’s baseline score to the amount of growth needed. |
Baseline score + the amount of growth needed = end-of-year goal 14 + 12 = 26 Colby’s end-of- year goal is 26 problems correct. |
Activity
Raymond is also a student in Ms. Wu’s class. Because his mathematics performance is significantly below grade level, she uses the first-grade computation measure to monitor his progress. Ms. Wu is going to use the intra-individual framework to determine Raymond’s end-of-year goal. Help Ms. Wu by calculating the information needed in each step of the intra-individual framework.
To complete this activity, use the following information:
- Raymond’s eight most recent test scores: 2, 3, 4, 4, 5, 5, 6, 6.
- Number of weeks left in the school year: 25
| Step | Enter your answer | Answer |
|
Median test score |
|
|
|
Current rate of improvement |
|
|
|
Expected rate of improvement |
|
|
|
Amount of growth needed |
|
|
|
Baseline score |
|
|
|
End-of-year goal |
|
|
