What evidence-based mathematics practices can teachers employ?
Page 5: Visual Representations
Yet another evidence-based strategy to help students learn abstract mathematics concepts and solve problems is the use of visual representations. More than simply a picture or detailed illustration, a visual representation—often referred to as a schematic representation or schematic diagram—is an accurate depiction of a given problem’s mathematical quantities and relationships. The purpose of this visual is to reflect a student’s understanding of the problem and to help her correctly solve it. For example, in the photo to the right, a student is using a visual representation—here, a pie chart—to learn about equivalent fractions. Despite the fact that teachers implement this strategy in the early grades to help students learn basic math facts, students with mathematics learning disabilities and difficulties often do not continue its use on their own to solve problems.
Research Shows
- Students who use accurate visual representations are six times more likely to correctly solve mathematics problems than are students who do not use them. However, students who use inaccurate visual representations are less likely to correctly solve mathematics problems than those who do not use visual representations at all.
(Boonen, van Wesel, Jolles, & van der Schoot, 2014) - Students with a learning disability (LD) often do not create accurate visual representations or use them strategically to solve problems. Teaching students to systematically use a visual representation to solve word problems has led to substantial improvements in math achievement for students with learning disabilities.
(van Garderen, Scheuermann, & Jackson, 2012; van Garderen, Scheuermann, & Poch, 2014) - Students who use visual representations to solve word problems are more likely to solve the problems accurately. This was equally true for students who had LD, were low-achieving, or were average-achieving.
(Krawec, 2014)
Visual representations are flexible; they can be used across grade levels and types of math problems. They can be used by teachers to teach mathematics facts and by students to learn mathematics content. Visual representations can take a number of forms. Click on the links below to view some of the visual representations most commonly used by teachers and students.
How does this practice align?
High-Leverage Practice (HLP)
- HLP15: Provide scaffolded supports
CCSSM: Standards for Mathematical Practice
- MP1: Make sense of problems and persevere in solving them.
Definition: A straight line that shows the order of and the relation between numbers.
Common Uses: addition, subtraction, counting
Definition: A bar divided into rectangles that accurately represent quantities noted in the problem.
Common Uses: addition, fractions, proportions, ratios
Definition: Simple drawings of concrete or real items (e.g., marbles, trucks).
Common Uses: counting, addition, subtraction, multiplication, division
Definition: Drawings that depict information using lines, shapes, and colors.
Common Uses: comparing numbers, statistics, ratios, algebra
Definition: Visual that assists students in remembering and organizing information, as well as depicting the relationships between ideas (e.g., word webs, tables, Venn diagrams).
Common Uses: algebra, geometry
| Triangles | ||
|---|---|---|
| equilateral | – all sides are same length – all angles 60° |
 |
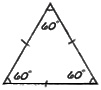| isosceles | – two sides are same length – two angles are the same |
 |
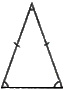| scalene | – no sides are the same length – no angles are the same |
 |
| right | – one angle is 90°(right angle) – opposite side of right angle is longest side (hypotenuse) |
 |
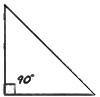| obtuse | – one angle is greater than 90° |  |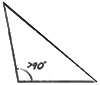
| acute | – all angles are less than 90° |  |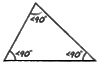
Before they can solve problems, however, students must first know what type of visual representation to create and use for a given mathematics problem. Some students—specifically, high-achieving students, gifted students—do this automatically, whereas others need to be explicitly taught how. This is especially the case for students who struggle with mathematics and those with mathematics learning disabilities. Without explicit, systematic instruction on how to create and use visual representations, these students often create visual representations that are disorganized or contain incorrect or partial information. Consider the examples below.
Elementary Example
Mrs. Aldridge ask her first-grade students to add 2 + 4 by drawing dots.
Talia draws the following:
Colby draws the following: 
Notice that Talia gets the correct answer. However, because Colby draws his dots in haphazard fashion, he fails to count all of them and consequently arrives at the wrong solution.
High School Example
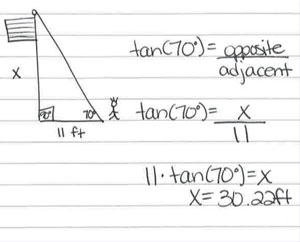
Mr. Huang asks his students to solve the following word problem:
The flagpole needs to be replaced. The school would like to replace it with the same size pole. When Juan stands 11 feet from the base of the pole, the angle of elevation from Juan’s feet to the top of the pole is 70 degrees. How tall is the pole?
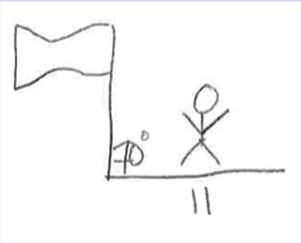
Compare the drawings below created by Brody and Zoe to represent this problem. Notice that Brody drew an accurate representation and applied the correct strategy. In contrast, Zoe drew a picture with partially correct information. The 11 is in the correct place, but the 70° is not. As a result of her inaccurate representation, Zoe is unable to move forward and solve the problem. However, given an accurate representation developed by someone else, Zoe is more likely to solve the problem correctly.
Brody
Zoe
Manipulatives
Some students will not be able to grasp mathematics skills and concepts using only the types of visual representations noted in the table above. Very young children and students who struggle with mathematics often require different types of visual representations known as manipulatives. These concrete, hands-on materials and objects—for example, an abacus or coins—help students to represent the mathematical idea they are trying to learn or the problem they are attempting to solve. Manipulatives can help students develop a conceptual understanding of mathematical topics. (For the purpose of this module, the term concrete objects refers to manipulatives and the term visual representations refers to schematic diagrams.)
It is important that the teacher make explicit the connection between the concrete object and the abstract concept being taught. The goal is for the student to eventually understand the concepts and procedures without the use of manipulatives. For secondary students who struggle with mathematics, teachers should show the abstract along with the concrete or visual representation and explicitly make the connection between them.
A move from concrete objects or visual representations to using abstract equations can be difficult for some students. One strategy teachers can use to help students systematically transition among concrete objects, visual representations, and abstract equations is the Concrete-Representational-Abstract (CRA) framework.
Concrete-Representational-Abstract Framework
The Concrete-Representational-Abstract (CRA) framework helps students gain a conceptual understanding of a mathematical process, rather than just completing the algorithm (e.g., 2 + 4, 2x + y = 27). Systematically connecting concrete objects or visual representations to the abstract equation is a way to scaffold a student’s understanding. The components of the framework are:
- Concrete —Students interact and manipulate three-dimensional objects, for example algebra tiles or other algebra manipulatives with representations of variables and units.
- Representational — Students use two-dimensional drawings to represent problems. These pictures may be presented to them by the teacher, or through the curriculum used in the class, or students may draw their own representation of the problem.
- Abstract — Students solve problems with numbers, symbols, and words without any concrete or representational assistance.
CRA is effective across all age levels and can assist students in learning concepts, procedures, and applications. When implementing each component, teachers should use explicit, systematic instruction and continually monitor student work to assess their understanding, asking them questions about their thinking and providing clarification as needed. Concrete and representational activities must reflect the actual process of solving the problem so that students are able to generalize the process to solve an abstract equation. The illustration below highlights each of these components.
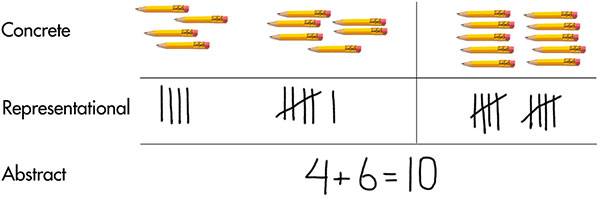
For Your Information
One promising practice for moving secondary students with mathematics difficulties or disabilities from the use of manipulatives and visual representations to the abstract equation quickly is the CRA-I strategy. In this modified version of CRA, the teacher simultaneously presents the content using concrete objects, visual representations of the concrete objects, and the abstract equation. Studies have shown that this framework is effective for teaching algebra to this population of students (Strickland & Maccini, 2012; Strickland & Maccini, 2013; Strickland, 2017).
Kim Paulsen discusses the benefits of manipulatives and a number of things to keep in mind when using them (time: 2:35).
Kim Paulsen, EdD
Associate Professor, Special Education
Vanderbilt University
Transcript: Kim Paulsen, EdD
Manipulatives are a great way of helping kids understand conceptually. The use of manipulatives really helps students see that conceptually, and it clicks a little more with them. Some of the things, though, that we need to remember when we’re using manipulatives is that it is important to give students a little bit of free time when you’re using a new manipulative so that they can just explore with them. We need to have specific rules for how to use manipulatives, that they aren’t toys, that they really are learning materials, and how students pick them up, how they put them away, the right time to use them, and making sure that they’re not distracters while we’re actually doing the presentation part of the lesson. One of the important things is that we don’t want students to memorize the algorithm or the procedures while they’re using the manipulatives. It really is just to help them understand conceptually. That doesn’t mean that kids are automatically going to understand conceptually or be able to make that bridge between using the concrete manipulatives into them being able to solve the problems. For some kids, it is difficult to use the manipulatives. That’s not how they learn, and so we don’t want to force kids to have to use manipulatives if it’s not something that is helpful for them. So we have to remember that manipulatives are one way to think about teaching math.
I think part of the reason that some teachers don’t use them is because it takes a lot of time, it takes a lot of organization, and they also feel that students get too reliant on using manipulatives. One way to think about using manipulatives is that you do it a couple of lessons when you’re teaching a new concept, and then take those away so that students are able to do just the computation part of it. It is true we can’t walk around life with manipulatives in our hands. And I think one of the other reasons that a lot of schools or teachers don’t use manipulatives is because they’re very expensive. And so it’s very helpful if all of the teachers in the school can pool resources and have a manipulative room where teachers can go check out manipulatives so that it’s not so expensive. Teachers have to know how to use them, and that takes a lot of practice.
