What evidence-based mathematics practices can teachers employ?
Page 6: Schema Instruction
 How does this practice align?
How does this practice align?
High-Leverage Practices
- HLP14: Teach cognitive and metacognitive strategies to support learning and independence
CCSSM: Standards for Mathematical Practice
- MP7: Look for and make use of structure.
Another effective strategy for helping students improve their mathematics performance is related to solving word problems. More specifically, it involves teaching students how to identify word problem types based on a given problem’s underlying structure, or schema. Before learning about this strategy, however, it is helpful to understand why many students struggle with word problems in the first place.
Difficulty with Word Problems
Most students, especially those with mathematics difficulties and disabilities, have trouble solving word problems. This is in large part because word problems require students to:
- Read and understand the text, including mathematics vocabulary
- Be able to identify and separate relevant information from irrelevant information
- Represent the problem correctly
- Choose an appropriate strategy for solving the problem
- Perform the computational procedures
- Check the answer to ensure that it makes sense
(Adapted from Stevens and Powell, 2016; Jitendra, et al., 2015; Jitendra et al., 2013)
Students who experience difficulty with any of the steps listed above, such as students who struggle with mathematics, will likely arrive at an incorrect answer.
Research Shows
- Students with mathematical difficulties and disabilities struggle more than their peers when solving word problems.
(Stevens & Powell, 2016; Jitendra et al., 2015; Fuchs et al., 2010) - Schema instruction—explicit instruction in identifying word problem types, representing them correctly, and using an effective method for solving them—has been found to be effective among students with mathematical difficulties and disabilities.
(Jitendra et al., 2016; Jitendra et al., 2015; Jitendra et al., 2009; Montague & Dietz, 2009; Fuchs et al., 2010) - Teaching students how to solve word problems by identifying word problem types is more effective than teaching them only to identify key words (e.g., “altogether,” “difference”).
(Jitendra, Griffin, Deatline-Buchman, & Sczesniak, 2007)
Word Problem Structures
To help students become more proficient at solving word problems, teachers can help students recognize the problem schema, which refers to the underlying structure of the problem or the problem type (e.g., adding or combining two or more sets, finding the difference between two sets). This, in turn, leads to an associated strategy for solving that problem type. There are two main types of schemas: additive and multiplicative. Below, we will introduce you to additive schemas before moving on to descriptions and examples of multiplicative schemas.
Additive Schemas
Additive schemas can be used for addition and subtraction problems. These schemas are effective for students in early elementary school through middle school. Below are a few examples of additive schemas used to solve word problems: total, difference, and change.
Description
- Involves adding or combining two or more distinct sets (each set representing a part) that are put together to form a total.
- Also known as part-part-whole or combine.
- Students might solve for any unknown in the equation.
- Can be used with a variety of types of numbers (e.g., whole, fractions, decimals).

Examples
Example 1:
Sam has 2 cookies. Ali has 3 cookies. How many cookies do they have altogether?
Solution equation: 
Example 2:
There are 6 students in the classroom and some more students in the hallway. There are 20 students in all. How many students are in the hallway?
Solution equation: 
Description
- Involves comparing and finding the difference between two sets.
- Also known as compare.
- Students might solve for any unknown in the equation.
- Can be used with a variety of types of numbers (e.g., whole, fractions, decimals).

Examples
Example 1:
The small dog has 3 spots. The large dog has 7 spots. How many more spots does the large dog have than the small dog?
Solution equation: 
Example 2:
Cy has 3 more pencils than Brody. Cy has 7 pencils. How many pencils does Brody have?
Solution equation: 
Example 3:
Ava has 9 fewer points than Giovani. Ava has 2 points. How many points does Giovani have?
Solution equation: 
Description
- Involves finding the increase or decrease in the quantity of the same set (i.e., there is one set and something happens to that set).
- Can involve multiple changes to the same set.
- Change schemas differ from total and difference schemas in that they involve a change in the set over time.
- Students might solve for any number in the equation.
- Can be used with a variety of types of numbers (e.g., whole, fractions, decimals).

Examples
Example 1:
Carly has 3 ribbons. Shay gives her 2 ribbons. How many ribbons does Carly have now?
Solution equation: 
Example 2:
Carly has 3 ribbons. She gave Shay 1 ribbon. How many ribbons does Carly have now?
Solution equation: 
Example 3:
Misha has 9 suckers. Kaheen gave her some more suckers. Now she has 12 suckers. How many did Kaheen give her?
Solution equation: 
Example 4:
Misha has some suckers. Kaheen gave her 4 suckers. Now Misha has 11 suckers. How many suckers did Misha have to begin with?
Solution equation: 
(Adapted from Stevens & Powell, 2016; Morales, Shute & Pellegrino, 1985)
For Your Information
Even when they apply the same schema to solve a word problem, students will likely approach its solution in a variety of ways. An example of this can be found below.
Problem: Emma had nine dollars. Then she earned some more money doing her chores. Now Emma has $12. How much money did she earn?
Two students, A and B, set up the problem using the change schema.

However, Student A solves the problem by subtracting 12 – 9. Student B solves the problem by counting on from 9. Although one student adds and the other subtracts, both students arrive at the correct solution. This example illustrates that the operation is secondary to the structure of the word problem.
Multiplicative Schemas
Multiplicative schemas can be used to solve multiplication and division problems. There are three main types of multiplicative schemas: equal, comparison, and ratio/proportion.
Description
- Involves multiplying or dividing groups where there is an equal number in each group.
- Students might solve for any unknown in the equation.
- Can be used with a variety of types of numbers (e.g., whole, fractions, decimals).
- Students often encounter these types of word problems on standardized tests during 3rd and 4th grades and on into middle school.
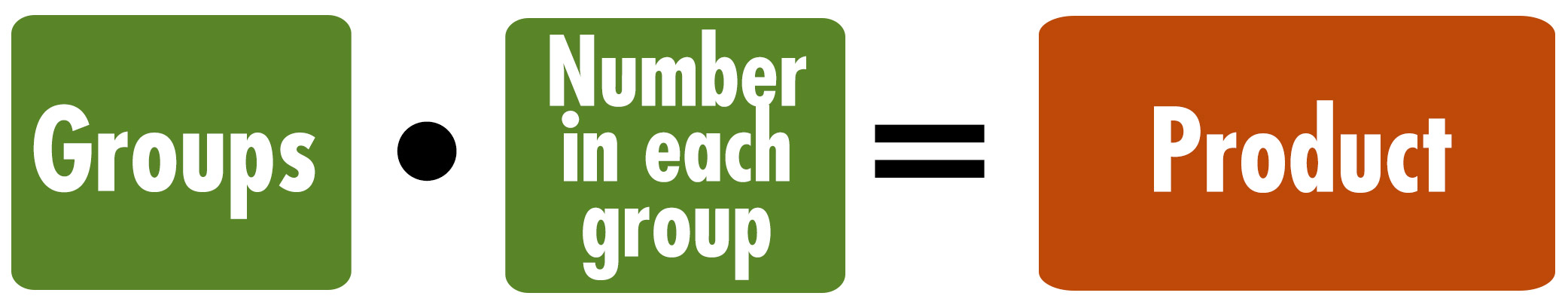
Examples
Example 1:
Tara has 6 bags of oranges. There are 4 oranges in each bag. How many oranges does Tara have?
Solution equation: 
Example 2:
Matthew has 20 comic books. His bookshelf has 5 shelves. He wants to put an equal number of comic books on each shelf. How many comic books will he put on each shelf?
Solution equation: 
Description
- Involves multiplying a set a given number of times.
- Students might solve for any unknown in the equation.
- Can be used with a variety of types of numbers (e.g., whole, fractions, decimals).
- Students often encounter these types of word problems on standardized tests during 4th and 5th grades and into middle school.

Examples
Example 1:
Tara has 6 bags of oranges. Mai has 6 pieces of candy. Kyla has 2 times as many pieces of candy. How many pieces of candy does Kyla have?
Solution equation: 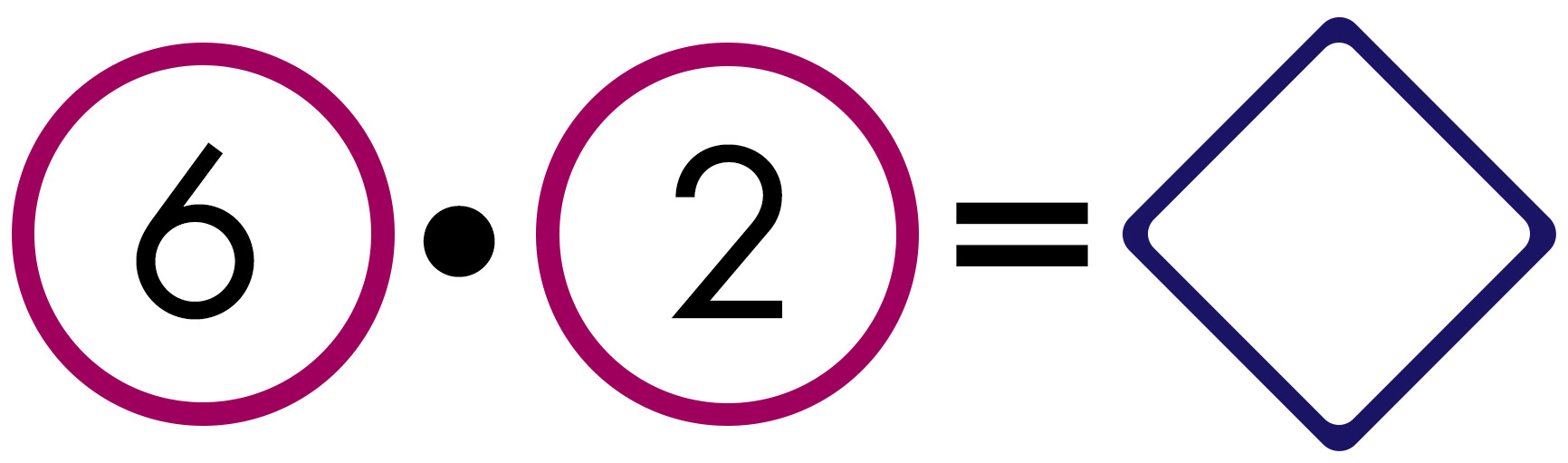
Example 2:
Pedro has 7 video games. Bronwynn has 21 video games. How many times as many video games does Bronwynn have than Pedro?
Solution equation: 
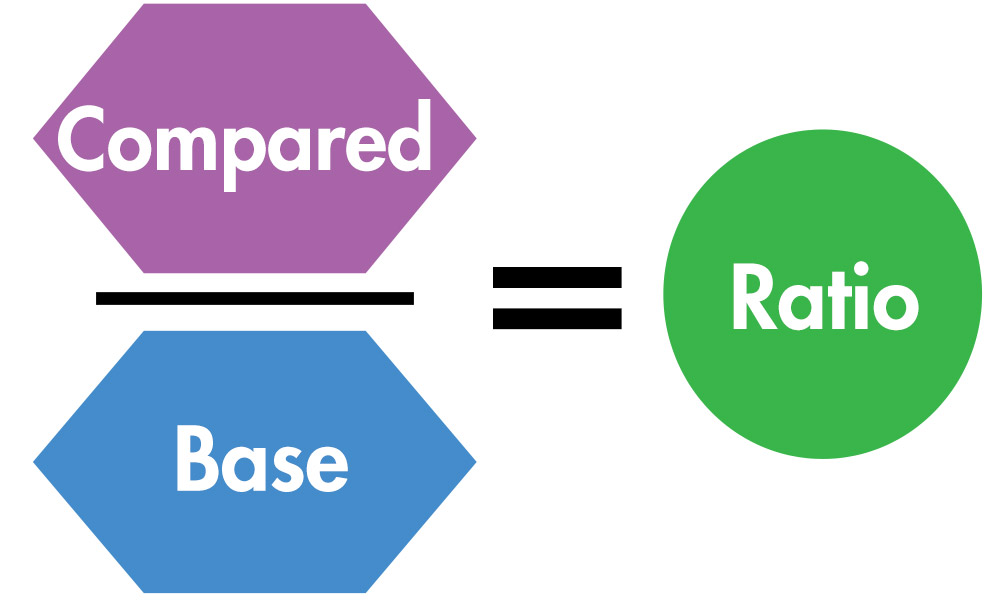
Description
- Involves finding the relationship between two numbers.
- Students might solve for any unknown in the equation.
- Can be used with a variety of types of numbers (e.g., whole, fractions, decimals).
- Students often encounter these types of word problems on standardized tests during upper elementary through middle school.
Example: On Saturday, Naoki worked in the hot sun for 10 hours, helping to clean up and revitalize a neighborhood park. To prevent dehydration, she took a 5-minute water break every hour. What proportion of time did Naoki spend working compared to taking breaks?
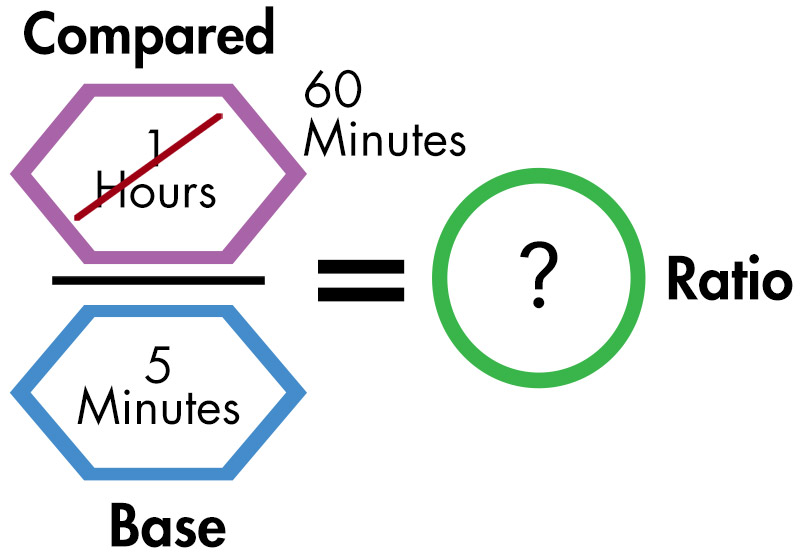
Note: To solve this problem, the student first converted hours to minutes so that he could work with the same unit.
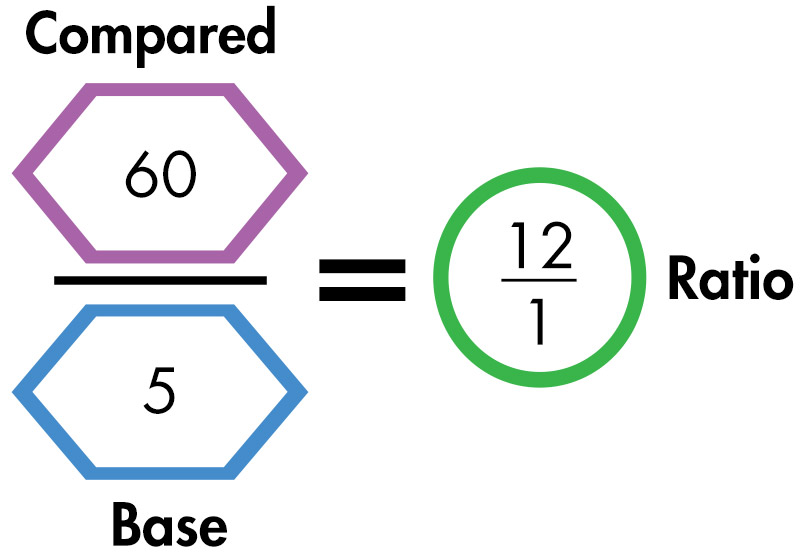
Note: The student determines that the ratio for working to taking breaks is 12 minutes of work to 1 minute on break.
Source: Jitendra, Star, Dupuis, & Rodriguez, 2013
Combined Schemas
As students advance in school, they will encounter new kinds of mathematical problems with new underlying structures, or schema. They will also encounter multi-step mathematics problems. The example below illustrates a percent change problem which involves the combination of two schemas: a multiplicative and an additive.
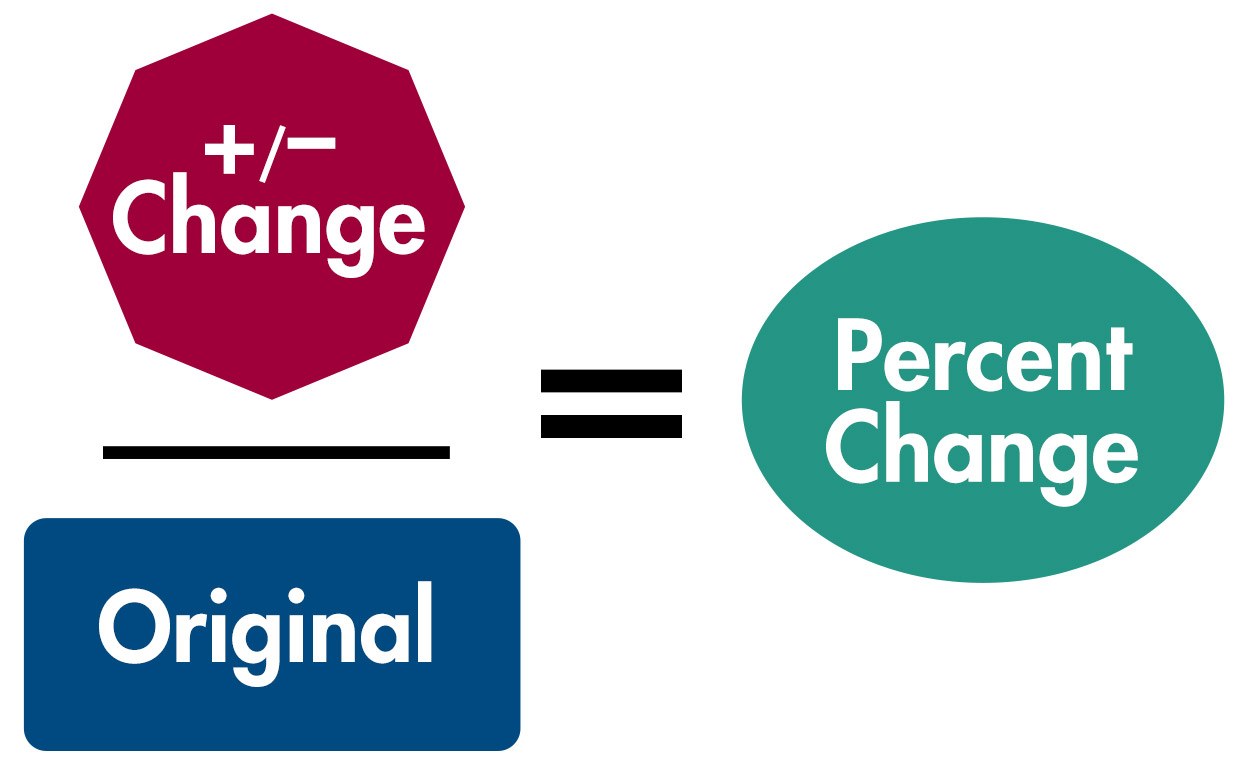

Note: After the student solves for the missing value in the equation above, he enters it along with the provided information in the equation below to solve the problem.
Example: Mark is interested in buying a car. The car costs $3,200. He will receive a 10% discount if he buys the car this weekend. How much will he pay for the car?
Solution equation (to determine the amount of change):
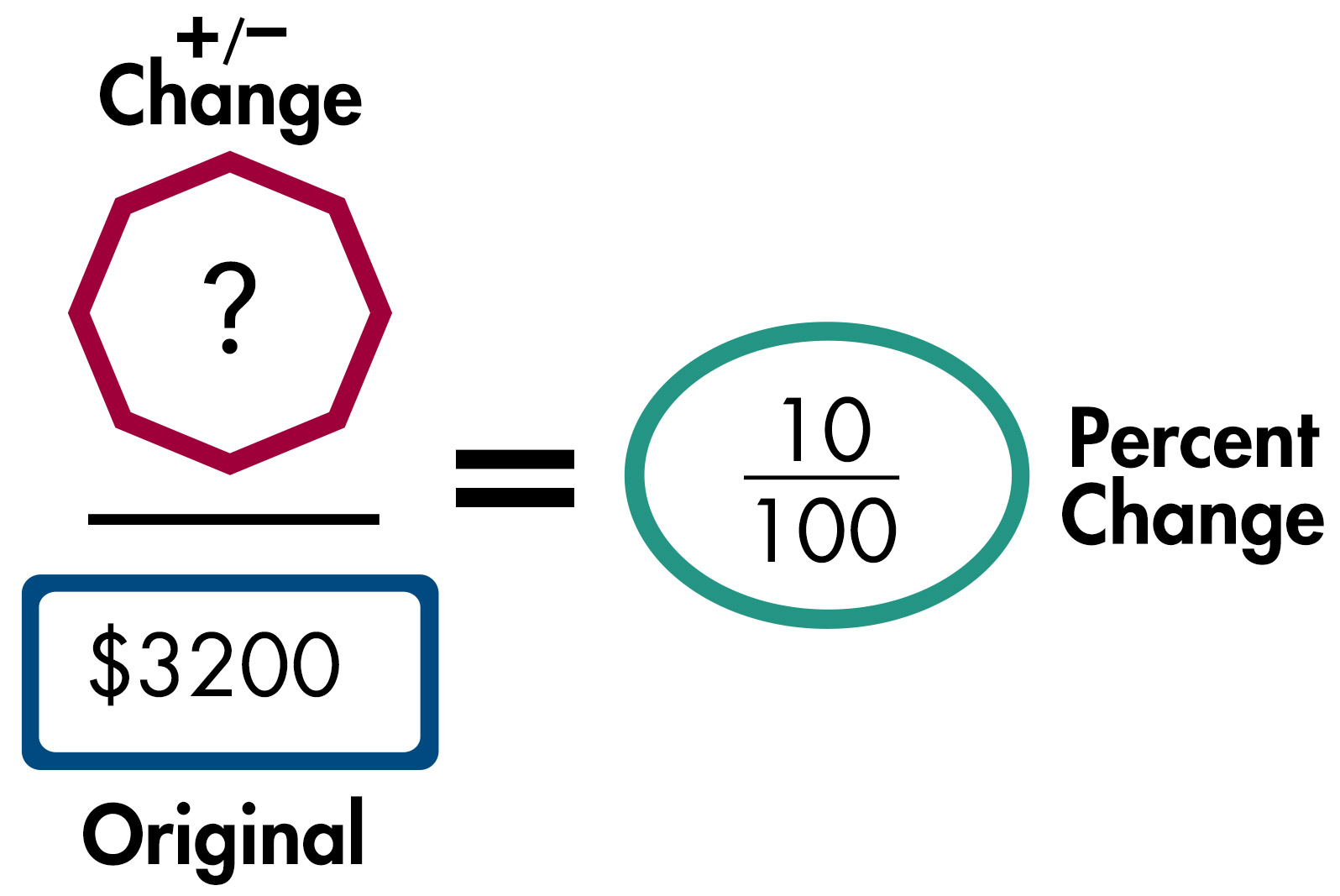
After the student solves for the “change,” which is $320, he will then create another solution equation to find the “new total.”
Solution equation (to determine the “new total”):

The student determines that with the 10% discount Mark will pay $2,880.
Sarah Powell, who has conducted extensive research on schema instruction, discusses the underlying focus of this strategy (time: 2:40).
Sarah Powell, PhD
Assistant Professor, Special Education
University of Texas at Austin

Transcript: Sarah Powell, PhD
The thing with schemas is that you cannot define word problems by their operation. So you cannot describe a word problem as being a subtraction problem or being a division problem. Instead, you have to describe the word problem at a deeper level and that is describing the word problem by its schema. And sometimes I like to use the word structure. It’s really important to use schemas or structures so that students have consistency with problem solving. If we teach the structure of combined problems in 1st grade and 2nd grade, students continue to see that schema in 3rd grade, 4th grade, and 5th grade. Now the numbers may get greater. So instead of adding three plus nine, they might be adding 133 plus 239. But the structure is the same. And so one of the things that we are trying to do with our math standards that guide most instruction in the United States is to provide consistency in math learning across grade levels, and the schemas really help do that, so you see that combined structure again and again.
Now in middle school grades, you see it in a slightly different way. It might be part of a multi-step problem, but it’s still there, so that every year we don’t have to reteach problem solving. We just help students say, “Oh, now we’re looking at a total schema but with fractions. Now here’s a total schema but with decimals.” And so there’s a lot of consistency that’s provided with the schemas. And right now problem solving is really taught grade-by-grade. So how do I solve 2nd-grade word problems, or how do I solve 5th-grade word problems? And that’s not a good way of thinking about it. It’s better if we focus on the schema and think about this grade-level continuum of problem solving. And they would just make problem solving so much easier for students and also easier for teachers, because then they’re not going back to square one every year and starting about how do I teach problem solving in 5th grade?
I would argue that problem solving is the most important thing you have to teach, because when we look at high-stakes assessments—and that’s where students show their mathematics competency—for word problems, students have to take the numbers and manipulate the numbers. It’s very difficult. Problem solving should be the primary focus of the mathematics curriculum, and instead of teaching problem solving as supplementary to math instruction, problem solving should really be taught as the way that we learn mathematics. And we need to get students to be thinkers of mathematics, not just doers of mathematics.
Teaching Word Problem Structures
As when teaching any strategy, teachers should use explicit, systematic instruction when introducing schema instruction, sometimes referred to as schema-based instruction (SBI). Although the same process is used to teach any schema, for illustrative purposes, the steps for how to teach the combine schema are outlined in the box below.
| Step1: Teach students to identify different problem types (e.g., combine) and practice translating the information into a diagram or equation. | |
| Descriptions | Example |
|
Start with one problem type or schema (e.g., combine). Start with stories that contain all the information (i.e., no unknown quantities). Show students how to translate the information for each problem type into a diagram (visual representation) or equation. |
Teach the students how to identify combine problems. LaTisha has 5 comic books. Riley has 3 more comic books. They have 8 comic books altogether.   |
| Step 2: Teach the students how to solve a word problem with an unknown quantity. | |
| Descriptions | Example |
|
Teach the students to use the following steps:
One method for doing this is to use the following mnemonic:
|
Calla has 4 cupcakes. Jaden has 6 cupcakes. How many cupcakes do they have altogether? Identify problem type: combine Translate into equation:  Solve problem:  |
| Step 3: Encourage student discourse | |
| Descriptions | Example |
|
Throughout the problem-solving process, the teacher should ask students to discuss how they solved the problem. |
Teacher: “Jayla, explain how you knew this problem type was combine”. |
(Adapted from Stevens & Powell, 2016)
Teachers should make sure that students have mastered one schema (e.g., combine) before introducing a different problem type (e.g., compare). This reduces the possibility of students confusing one schema type with another during the learning process.