What is RTI for mathematics?
Page 3: Universal Screening
The administration of an assessment to every student in a classroom, universal screening is used to determine which of those students are performing at grade level in mathematics and which of them are struggling. When they administer universal screening measures, schools or districts need to consider a number of important factors: the frequency of the screening, the selection of the screening measure, and the criteria used to determine which students are in need of intervention.
Frequency of the Screening
The universal screening is administered between one and three times per year, depending on district policy and the availability of resources. Whether given once a year or more often, its purpose changes slightly depending on the time at which it is administered, as is outlined in the table below.
| Time Administered | Purpose |
| Beginning of Year (September/October) |
|
| Middle of Year (January/February) |
|
| End of Year (April/May) |
|
For Your Information
- In the case of kindergarten and 1st-grade students, teachers might find it beneficial to delay the administration of universal screening measures until November. Doing so allows students ample time to acclimate to school, allows teachers to provide initial instruction, and reduces the possibility that students will be misidentified as struggling with mathematics.
- By the time students enter middle and high school, the intervention needs of most students have already been established. However, it is still important to conduct universal screenings to identify other students who might be struggling, including students who have moved from another district or state and students who begin to struggle later in school.
Selecting a Measure
The current research supports curriculum based measurement (CBM), sometimes referred to as general outcome measurement (GOM), as a reliable universal screening tool to identify students who may struggle with mathematics. Universal screening measures can consist of a computation probe, a concepts and applications probe, or both. Examples of each can be found below.
curriculum-based measurement (CBM)
A type of progress monitoring conducted on a regular basis to assess student performance throughout an entire year’s curriculum; teachers can use CBM to evaluate not only student progress but also the effectiveness of their instructional methods.
general outcome measurement (GOM)
A type of formative assessment in which multiple related skills are measured on a regular basis to assess a student’s performance on that skill across time.
| Computation Probe | Concepts and Applications Probe* | |
| Measures students’ procedural knowledge (e.g., their ability to add fractions). | Assesses conceptual understanding of mathematics or students’ ability to apply mathematics knowledge (e.g., to make change from a purchase). | |
 Elementary |
 Secondary |
 Elementary |
Sample Elementary Computation Probe
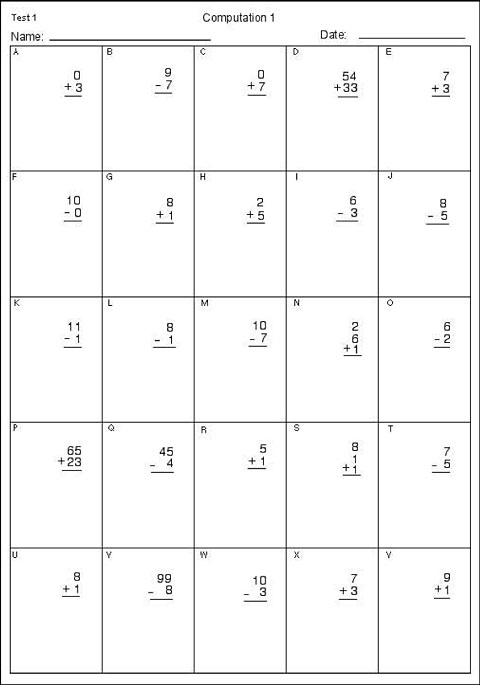
Sample Elementary Computation Probe: This probe is a white sheet of paper with spaces to fill in the student’s name and date across the top of the page. In the upper right-hand corner, the page is labeled “Test 1.” Underneath the name and date, the page is titled in the center “Computation.” The page is divided into five columns and five rows, with each computation problem labeled with a letter of the alphabet. The computation problems are adding two or three single-digit numbers, adding two two-digit numbers without regrouping, subtracting two single-digit numbers without regrouping, and subtracting a single-digit number from a two-digit number.
(Close this panel)
Sample Secondary Computation Probe
The sample secondary computation probe below is designed to assess students’ basic algebraic skills. Note that a normal probe would contain 60 questions and allow students five minutes to complete them. This 30-item example, which is the first of a two-page probe, is presented here for the sake of brevity and illustrative purposes.
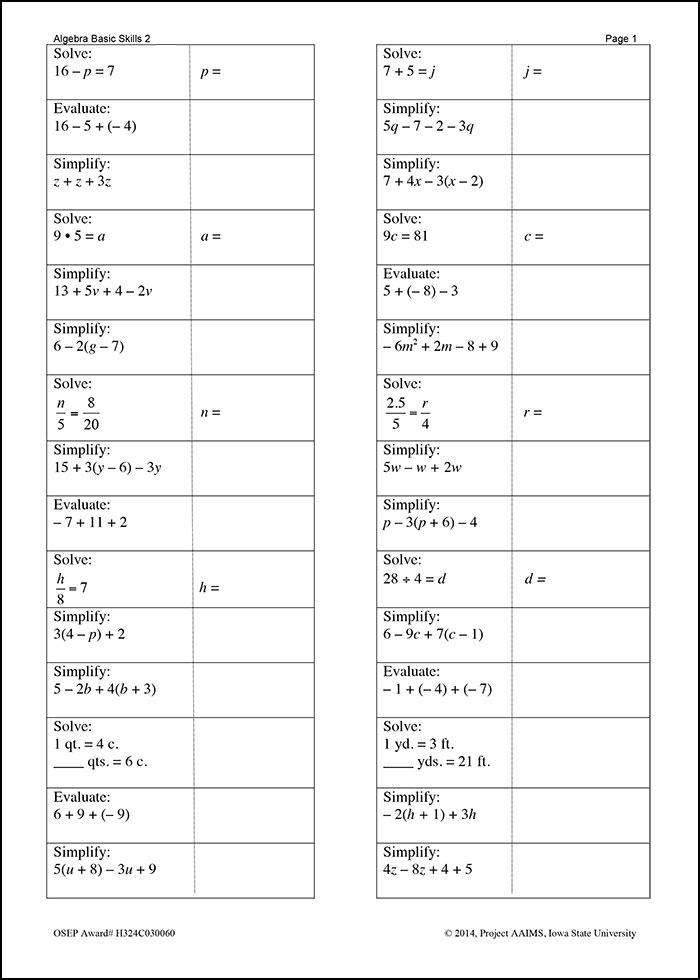
Project AAIMS. (2014). Project AAIMS algebra progress monitoring measures [Algebra Basic Skills, Algebra Foundations]. Ames, IA: Iowa State University, College of Human Sciences, School of Education, Project AAIMS.
This sample secondary computation probe is a single sheet featuring 30 mathematics problems. The questions ask students to solve simple equations (e.g., 16 minus p equals 7, p equals), use the distributive property [e.g., 16 minus 5 plus (negative 4)] , compute with integers (e.g., 9 times 5 equals a), combine like terms (13 plus 5v plus 4 minus 2v), and use proportional reasoning (n over 5 equals 8 over 20, n equals). The top of the sheet is labeled “Algebra Basic Skills 2, Page 1.” Note that this is the first of a two-page computation probe containing 60 questions.
(Close this panel)
Sample Elementary Concepts and Applications Probe
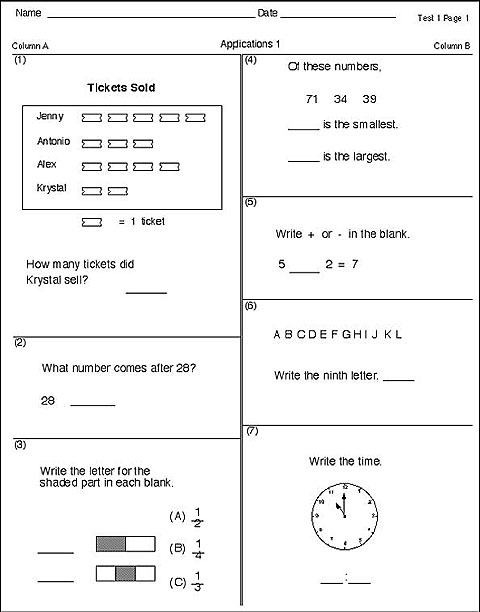
Sample Elementary Concepts and Applications Probe: This graphic is of a sample concepts and applications probe. It is a white sheet of paper with spaces to fill in your name and date across the top of the page. In the upper right-hand corner the page is labeled, “Test 1 Page 1.” Underneath the name and date the page is titled in the center “Applications 1.” The page is divided into two columns, column A labeled on the left and column B labeled on the right. Column A is divided into three uneven rectangles to delineate questions 1 through 3. Question 1 shows the title, Tickets Sold, with a picture graph below. Four names are listed—Jenny, Antonio, and Alex, Krystal—with variable pictures of tickets lined up beside their names. Underneath the names is a key, showing a picture of one ticket as equal to 1 ticket. Below the picture graph is the question: How many tickets did Krystal sell?, with a space to put an answer. There is a dividing line before question 2. Question 2 asks “What number comes after 29?” Below the question is the number 29 with a space to the right of the number to place an answer. There is another dividing line before question 3. Question 3 states “Write the letter for the shaded part in each blank.” Two blanks are provided, one on top of the other. To the right of each blank is a rectangle that is partly shaded. To the right of the shaded rectangles are three answer choices, one on top of the other. Answer choice A is 1/2, answer choice B is 1/4, and answer choice C is 1/3. Column B is divided into four uneven rectangles to delineate questions 4 through 7. Question 4 has the beginning phrase “Of these numbers…” then the numbers 71, 34, and 39 written below. Below the numbers is a blank then the text “is the smallest?” Below that statement is another blank and the text “is the largest?” There is a dividing line and then question 5 which states “Write + or – in the blank.” Below the text is the following incomplete number sentence: 5_____2 = 7. Question 6 begins under another dividing line and lists the alphabet letters ABCDEFGHIJKL. Below the letters is the statement “Write the ninth letter” with a blank to the right of the statement to fill in an answer. The last question, question 7, begins after the dividing line. It states “Write the time.” There is a picture of a clock with the hour hand pointing to the 10 and the minute hand pointing to the 12. Below the clock is a blank, then a colon, and another blank to record the time on the clock.
(Close this panel)
* No valid middle or high school concepts and applications probes are available at this time.
As an alternative to GOM, existing data (e.g., year-end tests, standardized achievement test scores) can be used for students in the 6th grade and above to identify those who might be struggling. Regardless of the universal screening measure a school chooses, that measure must:
- Align with state mathematics standards for a given grade
- Be feasible to administer given expense, time, and training constraints
- Accurately identify struggling students
For Your Information
The National Center on Intensive Intervention provides a tools chart that presents information about commercially available progress monitoring probes that have been reviewed by a panel of experts and rated on key features. Click here to use this tool chart.
There is a lack of available validated measures to assess the mathematics skills of high school students. Brad Witzel highlights the need for better universal screening assessments at the high school level and offers suggestions to confirm universal screening data (time: 1:10).
Transcript: Brad Witzel, PhD
First, it’s important that no matter what grade level we have valid universal screening solutions, but too often the screeners that we’re using focus solely on computational outcomes without reasoning at a level complex enough to address the needs of middle school and secondary math content. Moreover, there are few universal screeners that have even been validated at this point for secondary mathematics. So, first, we need more and better conceptually infused assessments to determine how well students understand math content. However, again, such assessments are difficult to develop. One suggestion that I have is that teachers with experience and expertise in formative assessment should compare their data to whatever universal screener that their school has chosen. By comparing their formative assessment, if done well with the universal screener outcome, they’ll develop a sort of triangulation of data that either confirms or denies the findings of that screener. Then an informed team could go through the problem-solving process to determine what is best for the student.
Administering a Measure
Teachers should schedule the administration of the universal screening assessment to fit their schedules and their classrooms’ needs. In the early grades—kindergarten and 1st grade—individual administration is required when assessing skills such as oral counting, identifying numbers, or identifying the larger number in a pair. For students in the 2nd grade and beyond, mathematics probes can generally be administered in a group setting. The amount of time it takes to administer a probe depends on the grade level and the type of measure in question. Computation probes can typically be administered in two to ten minutes, whereas concepts and application probes take five to ten minutes to complete. When available, computer-based screening measures are recommended. Regardless of the type of assessment used, alternate forms are administered if multiple screenings are conducted across the year (e.g., at the beginning, middle, and end of the year).
alternate form
An assessment that measures the same skills and has the same format as the standard version, but that features different items.
David Allsopp discusses how time, staffing, and scheduling affect universal screening at the high school level (time: 1:26).
David Allsopp, PhD
Assistant Dean for Education and Partnerships
University of South Florida
Transcript: David Allsopp, PhD
There are issues, and time is a big one. Because of the structure of elementary schools, we have, typically, a teacher with a classroom of kids who has them for multiple periods. There’s more possibility of time for kids to engage in universal screening at the middle and high school levels. Things aren’t structured that way. In terms of trying to find that time, from my perspective it needs to be a part of the school calendar and schedule, and that needs be done up front. Part of the issue, too, is how staffing occurs. So where students are placed within classrooms really should be predicated on that universal assessment. But that oftentimes happens before the universal assessment happens. Some schools base next year’s scheduling in terms of where students are placed on the prior year’s benchmark assessment, and that becomes their universal screening device. And I think many schools are using that simply because it’s the easiest thing to do, and it’s less complicated in terms of trying to schedule these assessments early in the year or even before kids begin school or before the schedule is made. So the scheduling factor is really an important variable within the whole concept of universal screening.
Criteria for Identifying Struggling Students
The criteria for determining which students are experiencing mathematics difficulties will depend on what measure is selected. Commercially available universal screening measures use benchmarks (or “cut points”). Students who score below these benchmarks may require additional intervention. Note: The administration and scoring of CBM probes is discussed in detail later in the module.
benchmark
An indicator used to identify the expected understandings and skills by grade level.
Listen as Lynn Fuchs explains the importance of setting benchmarks or cut points high enough that students who are likely to struggle with mathematics will be identified (time: 0:44).
Lynn Fuchs, PhD
Dunn Family Chair in Psychoeducational Assessment
Department of Special Education
Vanderbilt University
Transcript: Lynn Fuchs, PhD
We want to have an objective source of information for predicting who will have difficulty. The biggest problem in screening is false positives. We tend to, in the earlier grades, identify a lot of students who look like they’re at risk and really will do nicely without any intervention services. But there also is the problem of false negatives, kids who don’t fail the screen and go on to develop difficulties. So we screen everybody, set the cut point high enough so that we don’t miss any students who have any chance of going on to develop difficulty.
