How can school personnel use data to make instructional decisions?
Page 7: Error Analysis for Mathematics
 Error analysis can also be conducted for mathematics, for computation as well as for concepts. There are a number of benefits to conducting an error analysis in mathematics. The teacher can:
Error analysis can also be conducted for mathematics, for computation as well as for concepts. There are a number of benefits to conducting an error analysis in mathematics. The teacher can:
- Identify the steps a student can perform correctly (as opposed to marking answers as correct or incorrect, which might mask the steps the student can perform correctly)
- Identify patterns of errors
- Determine whether the error is a one-time miscalculation or whether it is a persistent error indicating an important misunderstanding of a math concept or operation
To conduct an error analysis for mathematics, the teacher can analyze the student’s errors on a worksheet, test, or progress monitoring measure. The teacher should score each problem, marking each incorrect digit in the student’s answer from RIGHT to LEFT for addition, subtraction, and multiplication problems. By scoring from right to left, the teacher can be sure to note incorrect digits in the place value columns. Division problems should be scored LEFT to RIGHT. Evaluating each numeral in the answer allows the teacher to gain more information.
Cole’s Math Worksheet
This document is an example of Cole’s mathematics classwork. It consists of 25 mathematics problems, some of which Cole’s teacher has marked as incorrect. The problems are as follows: Problem 1 is 105 plus 25. Cole has answered 130, showing how he regrouped to solve the problem. Problem 2 is 47 minus 39. Cole has answered 12, a response he reached by subtracting the 7 from the 9 without regard to their position in the problem. The teacher has marked out both numbers of the 12 with a blue pen. Problem 3 is 312 minus 0. Cole has correctly answered 312. Problem 4 is 98 minus 1, and Cole has recorded the correct answer, 97. Problem 5 is 26 minus 12. Cole has correctly answered 14. Problem 6 is 154 minus 80, but Cole’s response, 134, is incorrect. His teacher has marked out all three numbers in his response with a blue pen. Problem 7 is 406 minus 295. Cole has incorrectly answered 291, and his teacher has marked out the 2 and the 9 with a blue pen. Problem 8 is 126 minus 29. Cole has incorrectly responded 103. His teacher has marked out all three numbers in his answer with a blue pen. Problem 9 is 13 plus 7. Cole has correctly answered 20, showing how he regrouped to solve the problem. Problem 10 is 409 plus 80, and Cole has correctly answered 489. Problem 11 is 375 plus 301, and Cole has correctly answered 676. Problem 12 is 432 minus 189, but Cole has incorrectly answered 366, all three digits of which his teacher has marked out with blue pen. Problem 13 is 222 plus 100, and Cole has correctly answered 322. Problem 14 is 59 minus 57, and Cole has correctly answered 2. Problem 15 is 68 plus 32, and Cole has correctly answered, showing how he regrouped to solve the problem. Problem 16 is 429 minus 421, which Cole has correctly answered as 008. Problem 17 is 109 minus 92. Cole’s answer, 197, is incorrect. His teacher has marked out all three digits of his response with a blue pen. Problem 18 is 416 minus 80. Cole’s answer, 376, is incorrect. His teacher has marked out the 7 with a blue pen. Problem 19 is 493 minus 36. Cole’s response, 463, is incorrect. His teacher has marked through the 6 and the 3 with a blue pen. Problem 20 is 272 minus 27. Cole’s answer, 255, is incorrect. His teacher has marked through the 5 in the tens position with a blue pen. Problem 21 is 211 minus 85. Cole’s response, 174, is incorrect. His teacher has marked through all three digits with a blue pen. Problem 22 is 305 plus 101. Cole’s answer, 406, is correct. Problem 23 is 219 minus 79, but Cole’s response, 260, is incorrect. His teacher has crossed through the 2 and the 6 with a blue pen. Problem 24 is 48 minus 18, which Cole answers correctly with 30. Finally, Problem 25 is 207 plus 111. Cole’s answer, 318, is correct.
For Your Information
- Unlike for reading in which the PRF is a general indicator of a student’s reading skills, there is no general indicator of a student’s mathematics skills.
- In the absence of appropriate progress monitoring measures or work samples, the National Center on Intensive Intervention provides information about ways to assess a student’s mathematics skills: counting, basic facts, place value concepts, whole-number computation, and fractions as numbers.
After marking the errors, it is important to analyze them further to help identify what types of errors have been made. Several of the most common errors students make with mathematical computation can be found in the table below.
| Common Types of Computation Errors | |
|---|---|
| Error Type | Example |
| Has not mastered basic number facts: The student does not know basic facts about addition, subtraction, multiplication, and division. |  The student isn’t fluent with basic number facts. The student isn’t fluent with basic number facts. |
| Misunderstanding of place value: The student records the answer so that the numbers are not in the appropriate column. | 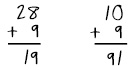 The student doesn’t understand place value. The student either added all the numbers together as in the first example or recorded the answer with the numbers reversed as in the second example. The student doesn’t understand place value. The student either added all the numbers together as in the first example or recorded the answer with the numbers reversed as in the second example. |
| Misunderstanding of regrouping: The student does not regroup, or he or she misapplies regrouping strategies. | 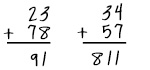 In the first example, the student added 8+3 correctly but didn’t regroup the “1” to the tens column. In the second example, the student either added left to right or didn’t regroup the “1” to the tens column but instead wrote “11.” In the first example, the student added 8+3 correctly but didn’t regroup the “1” to the tens column. In the second example, the student either added left to right or didn’t regroup the “1” to the tens column but instead wrote “11.” |
| Not regrouping with 0: When a problem contains one or more 0’s in the top number (minuend), the student is unsure what to do. | 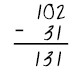 The student subtracts the 0 from the 3 instead of regrouping. The student subtracts the 0 from the 3 instead of regrouping. |
| Performing incorrect operation: Students often subtract when they are supposed to add or vice versa. However, students might also perform other incorrect operations, such as multiplying instead of adding. | 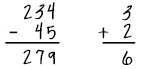 In the first example, the student added instead of subtracting. In the second example, the student multiplied instead of adding. In the first example, the student added instead of subtracting. In the second example, the student multiplied instead of adding. |
| Subtracting the lesser number from the greater number: Regardless of placement, the student always subtracts the lesser from the greater number. | 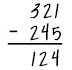 In each column, the student subtracted the lesser number from the greater number. In each column, the student subtracted the lesser number from the greater number. |
| Adding and subtracting fractions: The student fails to find the common denominator when adding or subtracting fractions. | 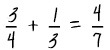 The student adds the numerators and then the denominators without finding the common denominator. The student adds the numerators and then the denominators without finding the common denominator. |
| Dividing Fractions: The student does not invert the second fraction (use the reciprocal) and multiply. | 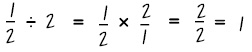 The student did not invert the 2 to ½ before multiplying to get the correct answer of ¼. The student did not invert the 2 to ½ before multiplying to get the correct answer of ¼. |
| Not aligning decimals when adding or subtracting: The student aligns the numbers without regard to where the decimal is located. | 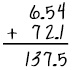 The student right justified the numbers without aligning the decimals. The student does not have a good understanding of place value. The student right justified the numbers without aligning the decimals. The student does not have a good understanding of place value. |
| Not placing decimal in appropriate place when multiplying or dividing: The student does not count the correct number of decimal places in the final answer. | 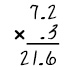 As with adding or subtracting, the student brought the decimal down instead of counting the number of digits to the right of the decimal points. As with adding or subtracting, the student brought the decimal down instead of counting the number of digits to the right of the decimal points. |
Common Types of Computational Errors
- The example is 7 plus 4, which the student has answered incorrectly with 13.
- The first example is 28 plus 9. The student’s answer, 19, is incorrect. The second example is 10 plus 9. The student’s answer, 91, is also incorrect.
- The first example is 23 plus 78. The student’s response, 91, is incorrect. The second example is 34 plus 57. The student incorrectly answers 811.
- The example is 102 minus 31. The student incorrectly answers 131.
- The first example is 234 minus 45, which the student incorrectly answers 279. The second example is 3 plus 2. The student’s answer, 6, is incorrect.
- The example is 321 plus 245. The student answers incorrectly with 124.
- The example is ¾ plus 1/3, which the student answers as 4/7.
- The equation in the example is ½ divided by 2 equals ½ times 2/1 equals 2/2 equals 1.
- The example is 6.45 plus 72.1, which the student has answered incorrectly as 137.5.
- The example is 7.2 times .3. The student’s answer, 21.6, is incorrect.
Now that you have reviewed several types of commonly occurring mathematical errors, let’s revisit Cole’s worksheet from above. Click here to review the worksheet.
Notice that the only problems that Cole answered incorrectly were subtraction problems. As we analyze these problems, it appears as though he always subtracts the lesser number from the greater number, regardless of whether the lesser number is on the top (minuend) or the bottom (subtrahend). The first three problems he answered incorrectly are described in the table below.
| Problems Analyzed from Coles’s Worksheet | ||
|---|---|---|
| Problem Number | Problem | Error |
| Problem 2 | 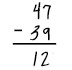 |
In the one’s column, Cole subtracted 7 from 9, instead of subtracting 9 from 7. Because he didn’t regroup, the 10’s column digit is also incorrect. |
| Problem 6 | 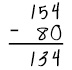 |
In the ten’s column, Cole subtracted 5 from 8, instead of 8 from 5. Because he didn’t regroup, the 100’s column digit is also incorrect. |
| Problem 7 | 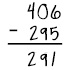 |
In the ten’s column, Cole subtracted 0 from 9 instead of 9 from 0. Because he didn’t regroup, the 100’s column digit is also incorrect. |
Problems Analyzed from Cole’s Worksheet
- The problem is 47 minus 39. Cole has answered 12.
- The problem is 154 minus 80. Cole has answered 134.
- The problem is 406 minus 295. Cole has answered 291.
![]() Teachers can also conduct an error analysis for algebra problems. Click here to review Systematic Analysis of Student Errors, a tool that teachers can use to identify the types of errors that students make consistently when solving algebra problems.
Teachers can also conduct an error analysis for algebra problems. Click here to review Systematic Analysis of Student Errors, a tool that teachers can use to identify the types of errors that students make consistently when solving algebra problems.
Activity
Now that you have seen how Cole’s incorrect problems were analyzed, it is time for you to practice analyzing Student 2’s mathematics errors. Click here to begin.
For this activity, click on each problem you wish to mark incorrect. For each incorrect response, analyze the correct and incorrect digits and try to determine the student’s error pattern(s). Next, in the description box below the probe, fill in the type(s) of errors Student 2 is making. After doing this, check your answer by clicking on the feedback link.
Student 2’s data seem to indicate that he fails to find the common denominator when adding fractions. He made this mistake on all of the problems he got incorrect, except for the problem 11. For this problem, it appears as though he made a careless error: He answered all other problems with a common denominator correctly.

(Close this panel)
Resources for Addressing Mathematics Skills
 The National Center on Intensive Intervention offers a collection of sample lessons and activities that can be used to develop and customize mathematics lessons to meet a student’s needs.
The National Center on Intensive Intervention offers a collection of sample lessons and activities that can be used to develop and customize mathematics lessons to meet a student’s needs.
